Cho tam giác đều \(ABC\) nội tiếp đường tròn \(\left( O \right)\). Độ dài của các cung \(AB,BC,CA\) đều bằng \(6\pi \). Diện tích của tam giác đều \(ABC\) là:

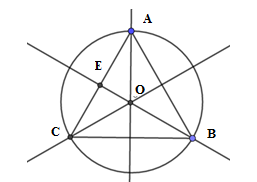
Gọi \(R\) là bán kính của đường tròn \(\left( O \right)\).  Độ dài của các cung \(AB,BC,CA\) đều bằng \(6\pi \) nên ta có \(C = 2\pi R = 6\pi  + 6\pi  + 6\pi  = 18\pi \), suy ra \(R = 9\) hay \(OA = OB = OC = 9\)

Ta cũng có  \(\widehat {AOB} = \widehat {BOC} = \widehat {COA} = {120^0}\) suy ra \(\Delta AOB = \Delta AOC = \Delta BOC\) suy ra \({S_{\Delta AOB}} = {S_{\Delta AOC}} = {S_{\Delta BOC}} = \dfrac{1}{3}{S_{\Delta ABC}}\)

Xét tam giác \(AOC\) có: \(\left\{ \begin{array}{l}\widehat {OAC} = \widehat {OCA} = {30^0}\\\widehat {COA} = {120^0}\end{array} \right.\)

Kẻ đường cao$OE$ , ta có đồng thời là đường trung tuyến, phân giác của góc \(\widehat {COA}\) . Ta có  \(\widehat {AOE} = \widehat {COE} = \dfrac{1}{2}\widehat {AOC}\)      

Xét tam giác $COE$ có:       \(\left\{ \begin{array}{l}\widehat {ECO} = {30^0}\\\widehat {CEO} = {90^0}\end{array} \right. \Rightarrow OE = \dfrac{1}{2}CO = \dfrac{R}{2}\)  

Áp dụng định lý Pytago ta có: \(CE = \sqrt {O{C^2} - O{E^2}}  = \sqrt {{R^2} - {{\left( {\dfrac{R}{2}} \right)}^2}}  = \dfrac{{\sqrt 3 }}{2}R\)      

Vậy \({S_{COE}} = \dfrac{1}{2}OE.CE = \dfrac{1}{2}.\dfrac{R}{2}.\dfrac{{\sqrt 3 R}}{2} = \dfrac{{\sqrt 3 {R^2}}}{8}\) 

Suy ra   \({S_{COA}} = 2{S_{COE}} = \dfrac{{\sqrt 3 {R^2}}}{4}\) và   \({S_{ABC}} = 3{S_{COA}} = \dfrac{{3\sqrt 3 {R^2}}}{4} = \dfrac{{3\sqrt 3 .{9^2}}}{4} = \dfrac{{243\sqrt 3 }}{4}\)