Câu hỏi:
3 năm trước
Cho hình vuông có cạnh là $6\,cm$ nội tiếp đường tròn $\left( O \right)$. Hãy tính diện tích hình tròn $\left( O \right)$.
Trả lời bởi giáo viên
Đáp án đúng: a
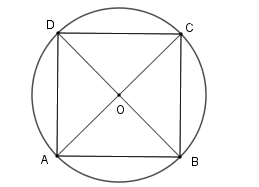
Gọi hình vuông \(ABCD\) nội tiếp đường tròn \(\left( O \right)\) khi đó $OA = OB = OC = OD = R \Rightarrow O$ là giao điểm của \(AC\) và \(BD\) \( \Rightarrow R = \dfrac{{AC}}{2}\) .
Xét tam giác vuông \(ABC\) ta có \(A{C^2} = A{B^2} + B{C^2} = {6^2} + {6^2} = 72 \Rightarrow AC = 6\sqrt 2 \)\( \Rightarrow R = \dfrac{{6\sqrt 2 }}{2} = 3\sqrt 2 \)
Diện tích hình tròn \(\left( O \right)\) là $S = \pi {R^2} = \pi {\left( {3\sqrt 2 } \right)^2} = 18\pi \,\left( {c{m^2}} \right)$
Hướng dẫn giải:
Áp dụng công thức tính diện tích hình tròn \(S = \pi {R^2}\)

