Cho đường tròn $\left( {O;R} \right)$ và một điểm $M$ sao cho $OM = R\sqrt 2 $. Từ $M$ vẽ các tiếp tuyến $MA,MB$ với đường tròn $(A,B$ là các tiếp điểm ). Tính diện tích giới hạn bởi hai tiếp tuyến $AM,MB$ và cung nhỏ $AB$.
Trả lời bởi giáo viên
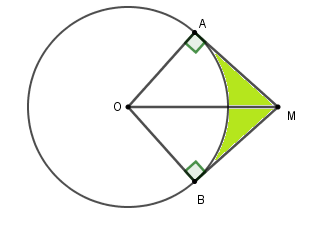
Xét \(\Delta OAM\) có \(AM = \sqrt {O{M^2} - O{A^2}} = \sqrt {2{R^2} - {R^2}} = R \)\(\Rightarrow {S_{OAM}} = \dfrac{{OA.AM}}{2} = \dfrac{{{R^2}}}{2}\)
Mà \(\Delta OAM = \Delta OBM\left( {c - c - c} \right)\)\( \Rightarrow {S_{OAMB}} = 2{S_{OAM}} = {R^2}\)
Xét \(\Delta OAM\) có \(\cos \widehat {AOM} = \dfrac{{OA}}{{OM}} = \dfrac{1}{{\sqrt 2 }} \)\(\Rightarrow \widehat {AOM} = 45^\circ \Rightarrow \widehat {AOB} = 2.45^\circ = 90^\circ \)
Diện tích quạt tròn \({S_{quạt\,AOB}} = \dfrac{{\pi {R^2}.90}}{{360}} = \dfrac{{\pi {R^2}}}{4}\)
Diện tích phần giới hạn bởi hai tiếp tuyến $AM,MB$ và cung nhỏ $AB$ là
\(S = {S_{OAMB}} - {S_{quạt\,AOB}} = {R^2} - \dfrac{{\pi {R^2}}}{4} \)\(= \dfrac{{\left( {4 - \pi } \right){R^2}}}{4}\)
Hướng dẫn giải:
Diện tích hình giới hạn bởi cung nhỏ $AB$ và $AM,MB$ là: \(S = {S_{OAMB}} - {S_{quạt\,AOB}}\)
Diện tích quạt tròn bán kính \(R\) và số đo cung \(n^\circ \) là \(S = \dfrac{{\pi {R^2}n}}{{360}}\)

