Câu hỏi:
3 năm trước
Cho đường tròn $\left( {O,8\,cm} \right)$, đường kính $AB.$ Điểm \(M \in (O)\) sao cho \(\widehat {BAM} = {60^0}\). Tính diện tích hình quạt $AOM$ .
Trả lời bởi giáo viên
Đáp án đúng: c
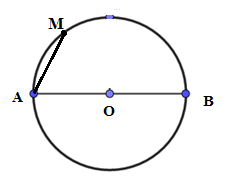
Xét đường tròn $\left( O \right)$ có\(\widehat {BAM} = 60^\circ \) suy ra số đo cung \(MB\) bằng \(2.60^\circ = 120^\circ \)
Suy ra số đo cung \(AM\) bằng \(n^\circ = 180^\circ - 120^\circ = 60^\circ \)
Vậy diện tích hình quạt $AOM$ là \(S = \dfrac{{\pi {R^2}n}}{{360}} = \dfrac{{\pi {{.8}^2}.60}}{{360}} = \dfrac{{32\pi }}{3}(c{m^2})\)
Hướng dẫn giải:
Sử dụng số đo góc nội tiếp (nhỏ hơn \(90^\circ \)) bằng nửa số đo cung bị chắn.
Sử dụng công thức tính diện tích hình quạt tròn có bán kính $R$ với số đo cung \({n^0}\): \({S_q} = \dfrac{{\pi {R^2}n}}{{360}} = \dfrac{{lR}}{2}\)

