Cho đường tròn $\left( O \right)$ đường kính $AB = $ $3\sqrt 3 $$cm$ . Điểm \(C \in (O)\) sao cho \(\widehat {ABC} = {60^0}\). Tính diện tích hình viên phân$BC$ . (Hình viên phân là phần hình tròn giới hạn bởi một cung tròn và dây căng cung ấy)

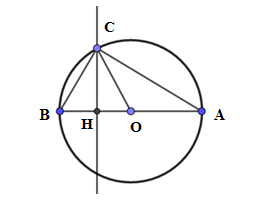
Xét đường tròn (O) có:

\(\widehat {ACB} = 90^\circ \) (góc nội tiếp chắn nửa đường tròn)

Suy ra \(\widehat {CAB} = 90^\circ  - \widehat {CBA} = 30^\circ \) (tam giác \(ABC\) vuông tại \(C\))

\(\widehat {ACB}\) và \(\widehat {BOC}\)   là góc nội tiếp và góc ở tâm cùng chắn cung $AC$  \( \Rightarrow \widehat {BOC} = 2.\widehat {ACB} = {2.30^0} = {60^0}\)\( \Rightarrow {S_{quạt\,\,AOC}} = \dfrac{{\pi {R^2}.60}}{{360}} = \dfrac{{\pi {R^2}}}{6}\)

Xét  \(\Delta BOC\) có   \(\widehat {BOC} = {60^\circ }\)  và  $\;OA = OC = R$ nên tam giác $AOC$ đều cạnh bằng $R$ .

Gọi $CH$ là đường cao của tam giác $AOC$ , ta có:

\(CH = CO.\sin {60^0} = \dfrac{{\sqrt 3 }}{2}.R\)\( \Rightarrow {S_{AOC}} = \dfrac{1}{2}CH.OA = \dfrac{1}{2}.\dfrac{{\sqrt 3 }}{2}.R.R \)\(= \dfrac{{\sqrt 3 }}{4}.{R^2}.\)

Diện tích hình viên phân $BC$ là:

${S_{quạt\,\,BOC}} - {S_{\Delta {\rm B}OC}} = \dfrac{{\pi {R^2}}}{6} - \dfrac{{\sqrt 3 }}{4}.{R^2} $$= \left( {\dfrac{\pi }{6} - \dfrac{{\sqrt 3 }}{4}} \right).{R^2} $$= \left( {\dfrac{{2\pi  - 3\sqrt 3 }}{{12}}} \right).{\left( {\dfrac{{3\sqrt 3 }}{2}} \right)^2} $$= \dfrac{{18\pi  - 27\sqrt 3 }}{{16}}\left( {c{m^2}} \right)$.