Câu hỏi:
2 năm trước
Cho $A,B,C,D$ là 4 đỉnh của hình vuông có cạnh là \(2cm\). Tính diện tích của hình hoa $4$ cánh giới hạn bởi các đường tròn có bán kính bằng \(a\), tâm là các đỉnh của hình vuông.
Trả lời bởi giáo viên
Đáp án đúng: a
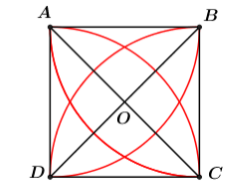
Ta có diện tích của hình hoa cần tính bằng $4$ lần diện tích của hình viên phân $AC$: \(S = 4{S_{viên\,phân\;AC}}.\)
Hình viên phân AC bằng \({S_{quạt\,ADC}} - {S_{\Delta ADC}}\)
Quạt tròn \(ADC\) có bán kính \(DA = DC = 3cm\) và số đo cung \(90^\circ \)
Có: \({S_{viên\,phân\;AC}} = {S_{quạt\;ADC}} - {S_{\Delta ADC}} \)\(= \dfrac{{\pi {R^2}{{.90}^0}}}{{{{360}^0}}} - \dfrac{1}{2}{R^2} \)\(= \left( {\dfrac{\pi }{4} - \dfrac{1}{2}} \right){R^2} \)\(= \dfrac{{\pi - 2}}{4}{.2^2} = \pi - 2\)\( \Rightarrow S = 4{S_{viên\,phân\;AC}} = 4.\left( {\pi - 2} \right) = 4\pi - 8.\)
Hướng dẫn giải:
Áp dụng công thức tính diện tích quạt tròn: \(S = \dfrac{{\pi {R^2}n}}{{360}}.\)
