Câu hỏi:
2 năm trước
Cho đường tròn $\left( O \right)$ đường kính \(AB = 2\sqrt 2 \;cm\). Điểm \(C \in (O)\) sao cho \(\widehat {ABC} = {30^0}\). Tính diện tích hình giới hạn bởi đường tròn $\left( O \right)$ và $AC,BC$ .
Trả lời bởi giáo viên
Đáp án đúng: a
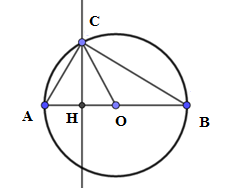
Diện tích hình tròn $\left( O \right)$ là: \({S_{(O)}} = \pi {R^2}\)
Ta có góc \(\widehat {ACB}\) là góc nội tiếp chắn nửa đường tròn \( \Rightarrow \widehat {ACB} = {90^0}\)\( \Rightarrow \widehat {BAC} = {90^0} - \widehat {CBA} = {90^0} - {30^0} = {60^0}.\)
Tam giác $AOC$ có \(\widehat {CAO} = {60^\circ }\) và $OA = OC = R$ nên tam giác $AOC$ đều cạnh bằng $R$ .
Giả sử $CH$ là đường cao của tam giác $ABC$ , ta có:
\(CH = CO.\sin {60^0} = \dfrac{{\sqrt 3 }}{2}.R \Rightarrow {S_{ABC}} = \dfrac{1}{2}CH.AB\)
$= \dfrac{1}{2}.\dfrac{{\sqrt 3 }}{2}R.2R$
\(= \dfrac{{\sqrt 3 }}{2}{R^2}.\)
Diện tích hình giới hạn bởi đường tròn $\left( O \right)$ và $AC,BC$ là:
$\dfrac{1}{2}{S_{(O)}} - {S_{ABC}} = \dfrac{1}{2}\pi {R^2} - \dfrac{{\sqrt 3 }}{2}{R^2} = \dfrac{1}{2}\left( {\pi - \sqrt 3 } \right){R^2} = \dfrac{1}{2}\left( {\pi - \sqrt 3 } \right){\left( {\sqrt 2 } \right)^2} = \pi - \sqrt 3 .$
Hướng dẫn giải:
Diện tích hình giới hạn bởi đường tròn $\left( O \right)$ và $AC,BC$ là: \(S = \dfrac{1}{2}{S_{(O)}} - {S_{ABC}}\)
