Tính \(CD\)?
Ta có: \( CD = ED - EC = 10\sqrt 6 - 10\sqrt 2 \)\(= 10\sqrt 2 \left( {\sqrt 3 - 1} \right)\,\,\,cm \approx 10,35\,\,cm\)
Tính \(CE.\)?
Áp dụng định lý Pitago cho\(\Delta BEC\) vuông tại \(E\) ta có:
\(\begin{array}{l}EC = \sqrt {B{C^2} - B{E^2}} = \sqrt {{{20}^2} - {{\left( {10\sqrt 2 } \right)}^2}} \\ = 10\sqrt 2 \,\,cm.\end{array}\)
Tính \(BE\)?
Áp dụng định lý Pitago cho \(\Delta ABD\) vuông tại \(A\) ta có:
\(DB = \sqrt {A{B^2} + A{D^2}} = \sqrt {{{20}^2} + {{20}^2}} = 20\sqrt 2 \,\,cm.\)
Mà \(\Delta ABD\) có \(AB = AD = 20\,cm \Rightarrow \Delta ABD\) vuông cân tại\(A.\)
\( \Rightarrow \angle ABD = \angle ADB = {45^0}\) (tính chất tam giác cân).
Theo đề bài ta có: \(\left\{ \begin{array}{l}AB = AC = 20\,cm\\\angle ABC = {60^0}\end{array} \right. \Rightarrow \Delta ABC\) là tam giác đều.
\( \Rightarrow BC = 20\,cm;\,\,\,\angle BAC = \angle BCA = {60^0}.\)
Lại có: \(AC = AD = 20\,\,cm \Rightarrow \Delta ACD\) cân tại \(A\)
\(\begin{array}{l} \Rightarrow \angle ACD = \angle ADC = \dfrac{{{{180}^0} - \angle CAD}}{2} = \dfrac{{{{180}^0} - \left( {{{90}^0} - \angle BAC} \right)}}{2} = \dfrac{{{{180}^0} - \left( {{{90}^0} - {{60}^0}} \right)}}{2} = {75^0}.\\ \Rightarrow \angle EDB = \angle ADC - \angle ADB = {75^0} - {45^0} = {30^0}.\end{array}\)
Xét \(\Delta BED\) vuông tại \(E\) ta có:
\(\left\{ \begin{array}{l}BE = BD.\sin \angle EDB = 20\sqrt 2 .\sin {30^0} = 20\sqrt 2 .\dfrac{1}{2} = 10\sqrt 2 \,\,cm.\\ED = BD.cos\angle EDB = 20\sqrt 2 .cos{30^0} = 20\sqrt 2 .\dfrac{{\sqrt 3 }}{2} = 10\sqrt 6 \,\,cm.\end{array} \right.\)
Tính \(BE\)?
Áp dụng định lý Pitago cho \(\Delta ABD\) vuông tại \(A\) ta có:
\(DB = \sqrt {A{B^2} + A{D^2}} = \sqrt {{{20}^2} + {{20}^2}} = 20\sqrt 2 \,\,cm.\)
Mà \(\Delta ABD\) có \(AB = AD = 20\,cm \Rightarrow \Delta ABD\) vuông cân tại\(A.\)
\( \Rightarrow \angle ABD = \angle ADB = {45^0}\) (tính chất tam giác cân).
Theo đề bài ta có: \(\left\{ \begin{array}{l}AB = AC = 20\,cm\\\angle ABC = {60^0}\end{array} \right. \Rightarrow \Delta ABC\) là tam giác đều.
\( \Rightarrow BC = 20\,cm;\,\,\,\angle BAC = \angle BCA = {60^0}.\)
Lại có: \(AC = AD = 20\,\,cm \Rightarrow \Delta ACD\) cân tại \(A\)
\(\begin{array}{l} \Rightarrow \angle ACD = \angle ADC = \dfrac{{{{180}^0} - \angle CAD}}{2} = \dfrac{{{{180}^0} - \left( {{{90}^0} - \angle BAC} \right)}}{2} = \dfrac{{{{180}^0} - \left( {{{90}^0} - {{60}^0}} \right)}}{2} = {75^0}.\\ \Rightarrow \angle EDB = \angle ADC - \angle ADB = {75^0} - {45^0} = {30^0}.\end{array}\)
Xét \(\Delta BED\) vuông tại \(E\) ta có:
\(\left\{ \begin{array}{l}BE = BD.\sin \angle EDB = 20\sqrt 2 .\sin {30^0} = 20\sqrt 2 .\dfrac{1}{2} = 10\sqrt 2 \,\,cm.\\ED = BD.cos\angle EDB = 20\sqrt 2 .cos{30^0} = 20\sqrt 2 .\dfrac{{\sqrt 3 }}{2} = 10\sqrt 6 \,\,cm.\end{array} \right.\)
Tính \(BE;CE\).
Vì \(AE\) là tia phân giác góc \(A\) nên ta có:
\( \Rightarrow \dfrac{{BE}}{{AB}} = \dfrac{{EC}}{{AC}} = \dfrac{{BE + EC}}{{AB + AC}}\)\( = \dfrac{{BC}}{{AB + AC}} = \dfrac{{25}}{{15 + 20}} = \dfrac{5}{7}\)
\( \Rightarrow \left\{ \begin{array}{l}BE = \dfrac{5}{7}AB = \dfrac{5}{7}.15 = \dfrac{{75}}{7}\\EC = \dfrac{5}{7}AC = \dfrac{5}{7}.20 = \dfrac{{100}}{7}\end{array} \right..\)
Giải tam giác \(ABC\)
Áp dụng định lý Pytago cho \(\Delta ABC\) vuông tại \(A\) có:
\(A{B^2} + A{C^2} = B{C^2}\) \( \Leftrightarrow B{C^2} = {15^2} + {20^2} = 625\)\( \Rightarrow BC = 25\)
Xét \(\Delta ABC\) vuông tại \(A\) ta có:
\(sinB = \dfrac{{AC}}{{BC}} = \dfrac{{20}}{{25}} \Rightarrow \angle B \approx {53^0}8'\)
Vì \(\Delta ABC\) vuông tại \(A\) ta có:
\(\angle B + \angle C = {90^0}\)\( \Leftrightarrow {53^0}8' + \angle C = {90^0}\)\( \Leftrightarrow \angle C \approx {36^0}52'\)
Giải tam giác \(ABC\)
Áp dụng định lý Pytago cho \(\Delta ABC\) vuông tại \(A\) có:
\(A{B^2} + A{C^2} = B{C^2}\) \( \Leftrightarrow B{C^2} = {15^2} + {20^2} = 625\)\( \Rightarrow BC = 25\)
Xét \(\Delta ABC\) vuông tại \(A\) ta có:
\(sinB = \dfrac{{AC}}{{BC}} = \dfrac{{20}}{{25}} \Rightarrow \angle B \approx {53^0}8'\)
Vì \(\Delta ABC\) vuông tại \(A\) ta có:
\(\angle B + \angle C = {90^0}\)\( \Leftrightarrow {53^0}8' + \angle C = {90^0}\)\( \Leftrightarrow \angle C \approx {36^0}52'\)
Tính diện tích của tam giác ABC.
Ta có: \({S_{\Delta ABC}} = \dfrac{1}{2}.AH.BC = \dfrac{1}{2}.3,6.7,5 = 13,5\,\,c{m^2}.\)
Tính các góc B, C và đường cao AH của tam giác.
Áp dụng định lý Pitago cho \(\Delta ABC\) vuông tại \(A\) có:
\(A{B^2} + A{C^2} = B{C^2}\) \( \Leftrightarrow B{C^2} = {6^2} + 4,{5^2} = 56,25\)\( \Rightarrow BC = 7,5\,\,cm.\)
Xét \(\Delta ABC\) vuông tại \(A\) ta có:
\(sinB = \dfrac{{AC}}{{BC}} = \dfrac{{4,5}}{{7,5}} = \dfrac{3}{5} \Rightarrow \angle B \approx {36^0}52'\)
Vì \(\Delta ABC\) vuông tại \(A\) ta có:
\(\angle B + \angle C = {90^0} \Leftrightarrow {36^0}52' + \angle C = {90^0}\)\( \Leftrightarrow \angle C \approx {53^0}8'\)
Áp dụng hệ thức lượng trong \(\Delta ABC\) vuông tại \(A\) có đường cao \(AH\) ta có:
\(AH.BC = AB.AC\)\( \Leftrightarrow AH.7,5 = 4,5.6\)\( \Leftrightarrow AH = 3,6\)
Tính các góc B, C và đường cao AH của tam giác.
Áp dụng định lý Pitago cho \(\Delta ABC\) vuông tại \(A\) có:
\(A{B^2} + A{C^2} = B{C^2}\) \( \Leftrightarrow B{C^2} = {6^2} + 4,{5^2} = 56,25\)\( \Rightarrow BC = 7,5\,\,cm.\)
Xét \(\Delta ABC\) vuông tại \(A\) ta có:
\(sinB = \dfrac{{AC}}{{BC}} = \dfrac{{4,5}}{{7,5}} = \dfrac{3}{5} \Rightarrow \angle B \approx {36^0}52'\)
Vì \(\Delta ABC\) vuông tại \(A\) ta có:
\(\angle B + \angle C = {90^0} \Leftrightarrow {36^0}52' + \angle C = {90^0}\)\( \Leftrightarrow \angle C \approx {53^0}8'\)
Áp dụng hệ thức lượng trong \(\Delta ABC\) vuông tại \(A\) có đường cao \(AH\) ta có:
\(AH.BC = AB.AC\)\( \Leftrightarrow AH.7,5 = 4,5.6\)\( \Leftrightarrow AH = 3,6\)
Tính diện tích \(\Delta AHM\)
Vì \(AM\) là trung tuyến của tam giác \(ABC \Rightarrow M\) là trung điểm \(BC\)\( \Rightarrow BM = MC = \dfrac{{BC}}{2} \approx 3,66\)
Áp dụng hệ thức lượng cho \(\Delta ABC\) vuông tại \(A,\) có đường cao \(AH\) ta có:
\(AH.BC = AB.AC\)\( \Leftrightarrow AH.7,32 = 6.4,2\)\( \Leftrightarrow AH \approx 3,44\)
\(A{B^2} = BH.CB\)\( \Leftrightarrow {6^2} = BH.7,32\)\( \Leftrightarrow BH \approx 4,92\)
Ta có: \(BM + MH = BH \Leftrightarrow MH = 4,92 - 3,66 \approx 1,26\)
\({S_{\Delta AHM}} = \dfrac{1}{2}AH.MH \approx \dfrac{1}{2}.3,44.1,26 \approx 2,17\,\,\,\left( {đvdt} \right)\)
Giải tam giác vuông \(ABC\).
Xét \(\Delta ABC\) vuông tại \(A\) ta có:
\(AC = AB.tan\angle B = 6.tan{35^0} \approx 4,2\)
\(AB = BC.\cos \angle B \Rightarrow 6 = BC.\cos {35^0} \Rightarrow BC \approx 7,32\)
Vì \(\Delta ABC\) vuông tại \(A\) ta có:
\(\angle B + \angle C = {90^0} \Leftrightarrow {35^0} + \angle C = {90^0}\)\( \Leftrightarrow \angle C = {55^0}\)
Giải tam giác vuông \(ABC\).
Xét \(\Delta ABC\) vuông tại \(A\) ta có:
\(AC = AB.tan\angle B = 6.tan{35^0} \approx 4,2\)
\(AB = BC.\cos \angle B \Rightarrow 6 = BC.\cos {35^0} \Rightarrow BC \approx 7,32\)
Vì \(\Delta ABC\) vuông tại \(A\) ta có:
\(\angle B + \angle C = {90^0} \Leftrightarrow {35^0} + \angle C = {90^0}\)\( \Leftrightarrow \angle C = {55^0}\)
Cho tam giác \(ABC\) vuông tại \(A,\) chiều cao \(AH\). Chọn câu sai.
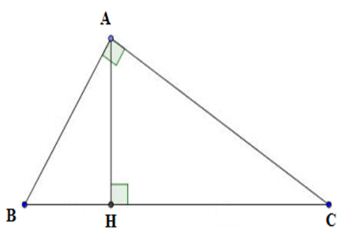
Ta thấy \(AH.BC = AB.AC\) nên D sai.
Cho hình vẽ sau:
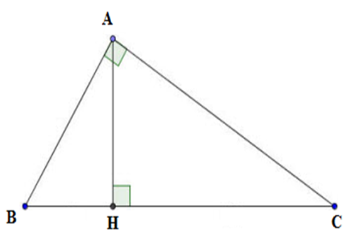
Chọn câu sai.
+ Xét tam giác \(AHB\) vuông tại \(H\) có \(\sin B = \dfrac{{AH}}{{AB}}\) nên A đúng.
+ Xét tam giác \(ABC\) vuông tại \(A\) có \(\cos C = \dfrac{{AC}}{{BC}}\) nên B đúng.
+ Xét tam giác \(ABC\) vuông tại \(A\) có \(\tan B = \dfrac{{AC}}{{AB}}\) nên C đúng.
+ Xét tam giác \(AHC\) vuông tại \(H\) có \(\tan C = \dfrac{{AH}}{{CH}}\) nên D sai.
Chọn câu đúng nhất. Nếu \(\alpha \) là một góc nhọn bất kỳ, ta có
Nếu \(\alpha \) là một góc nhọn bất kỳ thì \({\sin ^2}\alpha + {\cos ^2}\alpha = 1;\tan \alpha .\cot \alpha = 1\)
$\tan \alpha = \dfrac{{\sin \alpha }}{{\cos \alpha }};\cot \alpha = \dfrac{{\cos \alpha }}{{\sin \alpha }}$ nên cả A, B, C đều đúng
Cho \(\alpha ;\beta \) là hai góc nhọn bất kì và \(\alpha < \beta \). Chọn câu đúng.
Với \(\alpha ;\beta \) là hai góc nhọn bất kì và \(\alpha < \beta \) thì
\(\sin \alpha < \sin \beta ;\,\cos \alpha > \cos \beta ;\tan \alpha < \tan \beta ;\cot \alpha > \cot \beta .\)
Vậy A, B, D sai, C đúng.
Tính giá trị của \(x\) trên hình vẽ
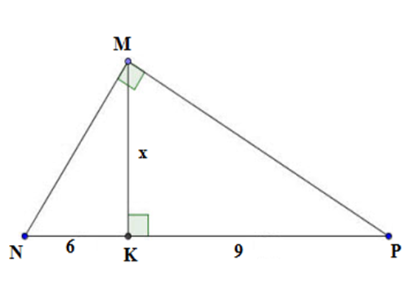
Xét tam giác \(MNP\) vuông tại \(M,\) có \(MK \bot NP\) ta có \(M{K^2} = NK.PK\) (hệ thức lượng trong tam giác vuông)
Hay \({x^2} = 6.9 \Leftrightarrow {x^2} = 54 \Rightarrow x = 3\sqrt 6 \,.\)
Cho \(\tan a = 3.\) Khi đó \(\cot a\) bằng
Ta có \(\tan a.\cot a = 1\) nên \(\cot a = \dfrac{1}{{\tan a}} = \dfrac{1}{3}.\)
Cho tam giác $ABC$ vuông tại $A$ có $AB = 3cm,{\rm{ }}BC = 5cm.{\rm{ }}AH$ là đường cao. Tính $BH,CH,AC$ và $AH.$
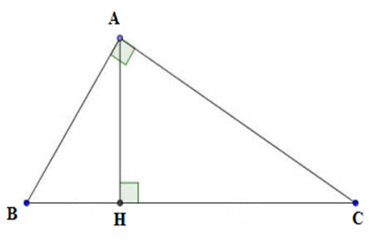
Xét tam giác \(ABC\) vuông tại \(A.\)
+ Theo định lý Pytago ta có \(A{B^2} + A{C^2} = B{C^2} \Leftrightarrow A{C^2} = {5^2} - {3^2} \Rightarrow AC = 4cm\)
+ Theo hệ thức lượng trong tam giác vuông ta có
\(A{B^2} = BH.BC \Rightarrow BH = \dfrac{{A{B^2}}}{{BC}} = \dfrac{{{3^2}}}{5} = \dfrac{9}{5} = 1,8cm\)
Mà \(BH + CH = BC \Rightarrow CH = BC - BH = 5 - 1,8 = 3,2\,cm.\)
Lại có \(AH.BC = AB.AC \Rightarrow AH = \dfrac{{AB.AC}}{{BC}} = \dfrac{{3.4}}{5} = 2,4cm\)
Vậy \(BH = 1,8\,cm\), \(CH = 3,2\,cm\), \(AC = 4\,cm\), \(AH = 2,4\,cm\)

