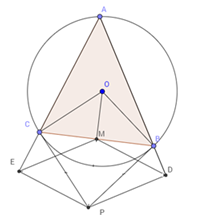
Góc \(MEP\) bằng với góc nào dưới đây?
Ta có M là trung điểm của cạnh BC $ \Rightarrow OM \bot BC$ (liên hệ đường kính và dây cung)
Ta có tứ giác BMPD nội tiếp ( vì \(\widehat {BDP}\)+ \(\widehat {BMP}\)=1800) \( \Rightarrow \widehat {MDP}\) = \(\widehat {MBP}\) (tính chất của tứ giác nội tiếp) (1)
Tương tự có tứ giác MCEP nội tiếp => \(\widehat {MEP}\) = \(\widehat {MCP}\) (tính chất của tứ giác nội tiếp) (2)
Mà tiếp tuyến tại B và C cắt nhau tại P nên dễ dàng suy ra được \(\Delta BPC\;\)cân tại P ( tính chất 2 tiếp tuyến cắt nhau)
\( \Rightarrow \widehat {MCP}{\rm{\;}} = \;\widehat {MBP}\;\left( 3 \right)\)
Từ (1); (2);(3) => \(\widehat {MEP}\) = \(\widehat {MDP}\)
Tính tổng diện tích các hình viên phân giới hạn bởi các cung nhỏ $CI,{\rm{ }}IB,{\rm{ }}BK,{\rm{ }}KC$ và các dây cung tương ứng của $\left( O \right)$ biết $AB = 20,{\rm{ }}BC = 24.$
Gọi diện tích hình cần tính là S, diện tích hình tròn (O) là \(S'\) , gọi giao điểm $BC$ và $IK$ là $M.$
Ta có ngay :
$\begin{array}{l}S = S' - {S_{ICKB}} = \pi I{O^2} - {S_{IBK}} - {S_{IKC}}\\ = \pi \dfrac{{I{K^2}}}{4} - \dfrac{{BM.IK}}{2} - \dfrac{{CM.IK}}{2}\\ = \pi \dfrac{{I{K^2}}}{4} - \dfrac{{BC.IK}}{2}.\end{array}$
Ta có :
\(\begin{array}{l}\;\;\;\;\;{S_{ABC}} = \dfrac{1}{2}AM.BC = \dfrac{{AB + BC + CA}}{2}.IM\\ \Leftrightarrow \sqrt {A{B^2} - B{M^2}} .24 = \left( {AB + BC + CA} \right).IM\\ \Leftrightarrow \sqrt {{{20}^2} - {{\left( {\dfrac{{24}}{2}} \right)}^2}} .24 = \left( {20.2 + 24} \right).IM\\ \Leftrightarrow IM = 6.\end{array}\)
Áp dụng hệ thức lượng trong tam giác \(IBM\) vuông tại \(B\) có đường cao \(BM\) ta có :
\(\begin{array}{l}B{M^2} = IM.MK \Leftrightarrow MK = \dfrac{{B{M^2}}}{{IM}} = \dfrac{{{{12}^2}}}{6} = 24.\\ \Rightarrow IM = IM + MK = 6 + 24 = 30.\\ \Rightarrow S = \dfrac{1}{4}\pi I{K^2} - \dfrac{1}{2}BC.IK = \dfrac{1}{4}\pi {.30^2} - \dfrac{1}{2}.24.30\\ = 225\pi - 360\;\;\left( {dvdt} \right).\end{array}\)
Chọn câu đúng.
+) Vì I là tâm đường tròn ngoại tiếp tam giác ABC nên IC là phân giác trong của góc C.
Vì K là tâm đường tròn ngoại tiếp tam giác ABC của góc A nên CK là phân giác ngoài của góc C.
Theo tính chất phân giác trong và phân giác ngoài ta có IC vuông CK nên $\widehat {ICK} = {90^0}$
Chứng minh hoàn toàn tương tự ta có: $\widehat {IBK} = {90^0}$
Xét tứ giác BICK ta có: \(\widehat {IBK} + \widehat {ICK} = {90^0} + {90^0} = {180^0}.\)
\( \Rightarrow BICK\) là tứ giác nội tiếp (tứ giác có tổng hai góc đối diện bằng \({180^0}\))
Do O là trung điểm của IK nên theo tính chất trung tuyến ứng với cạnh huyền bằng nửa cạnh huyền thì OC = OI = OK.
Vậy O là tâm đường tròn ngoại tiếp tứ giác IBKC hay bốn điểm B, I, C, K cùng thuộc (O)
+) Ta có : Tam giác IOC cân tại O nên : $\widehat {OIC} = \widehat {OCI}.$
Mặt khác, theo tính chất góc ngoài của tam giác ta có :
$\widehat {OIC} = \widehat {IAC} + \widehat {ACI} = \dfrac{1}{2}\widehat {BAC} + \dfrac{1}{2}\widehat {ACB} = \dfrac{1}{2}\widehat {BAC} + \dfrac{1}{2}\widehat {ABC}$
$ \Rightarrow \widehat {ICO} + \widehat {ICA} = \dfrac{1}{2}\widehat {BAC} + \dfrac{1}{2}\widehat {ABC} + \dfrac{1}{2}\widehat {ACB} = \dfrac{1}{2}{.180^0} = {90^0}$
$ \Rightarrow OC \bot CA.$
Do đó AC là tiếp tuyến của (O) tại C.
Cả A, B đều đúng.
Chọn câu đúng.

+) Vì I là tâm đường tròn ngoại tiếp tam giác ABC nên IC là phân giác trong của góc C.
Vì K là tâm đường tròn ngoại tiếp tam giác ABC của góc A nên CK là phân giác ngoài của góc C.
Theo tính chất phân giác trong và phân giác ngoài ta có IC vuông CK nên $\widehat {ICK} = {90^0}$
Chứng minh hoàn toàn tương tự ta có: $\widehat {IBK} = {90^0}$
Xét tứ giác BICK ta có: \(\widehat {IBK} + \widehat {ICK} = {90^0} + {90^0} = {180^0}.\)
\( \Rightarrow BICK\) là tứ giác nội tiếp (tứ giác có tổng hai góc đối diện bằng \({180^0}\))
Do O là trung điểm của IK nên theo tính chất trung tuyến ứng với cạnh huyền bằng nửa cạnh huyền thì OC = OI = OK.
Vậy O là tâm đường tròn ngoại tiếp tứ giác IBKC hay bốn điểm B, I, C, K cùng thuộc (O)
+) Ta có : Tam giác IOC cân tại O nên : $\widehat {OIC} = \widehat {OCI}.$
Mặt khác, theo tính chất góc ngoài của tam giác ta có :
$\widehat {OIC} = \widehat {IAC} + \widehat {ACI} = \dfrac{1}{2}\widehat {BAC} + \dfrac{1}{2}\widehat {ACB} = \dfrac{1}{2}\widehat {BAC} + \dfrac{1}{2}\widehat {ABC}$
$ \Rightarrow \widehat {ICO} + \widehat {ICA} = \dfrac{1}{2}\widehat {BAC} + \dfrac{1}{2}\widehat {ABC} + \dfrac{1}{2}\widehat {ACB} = \dfrac{1}{2}{.180^0} = {90^0}$
$ \Rightarrow OC \bot CA.$
Do đó AC là tiếp tuyến của (O) tại C.
Cả A, B đều đúng.
Gọi $MN$ là đường kính bất kì của đường tròn \(\left( O \right)\) sao cho ba điểm $S,{\rm{ }}M,{\rm{ }}N$ không thẳng hàng. Xác định vị trí của $MN$ để diện tích tam giác $SMN$ lớn nhất.
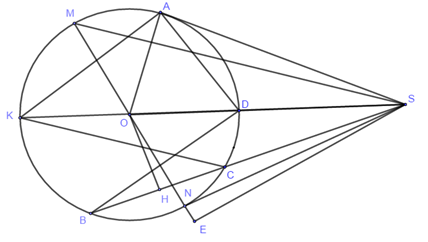
Kẻ \(SE \bot MN \Rightarrow {S_{SMN}} = \dfrac{1}{2}MN.SE\). Mà có \(MN\) cố định ($MN$ là đường kính của đường tròn)
Vậy nên \({S_{SMN}}\) max khi và chỉ khi $SE$ max
Xét \(\Delta SOE\) vuông tại E có \(SO\) là cạnh huyền , \(SE\) là cạnh góc vuông \( \Rightarrow SE \le SO \Rightarrow {S_{SMN}} \le \dfrac{1}{2}MN.SO\)
Dấu “=” xảy ra khi và chỉ khi \(SE\) trùng với \(SO\), suy ra \(SO \bot MN\).
Vậy diện tích tam giác$SMN$ lớn nhất khi và chỉ khi \(SO \bot MN\).
Chọn câu đúng.
Gọi \(D,K\) lần lượt là giao điểm của \(SO\) với đường tròn (\(D\) nằm giữa \(K\) và \(S\))
Xét đường tròn \(\left( O \right)\) có:
\(\angle SAD\) là góc tạo bởi tiếp tuyến và dây cung chắn cung \(AD\)
\(\angle AKS\) là góc nội tiếp chắn cung \(AD\).
Suy ra \(\angle SAD = \angle AKS\).
Xét \(\Delta SDA\) và $\Delta SAK$ có:
\(\angle KSA\) chung
\(\angle SAD = \angle AKS\) (cmt)
\( \Rightarrow \Delta SDA \backsim \Delta SAK \Rightarrow \dfrac{{SA}}{{SK}} = \dfrac{{SD}}{{SA}} \Rightarrow S{A^2} = SK.SD\). (1)
Xét \(\Delta KCS\) và \(\Delta BDS\) ta có:
\(\angle AKC = \angle DBS\) (hai góc nội tiếp cùng chắn cung DC)
\(\angle DSC\) chung
\( \Rightarrow \Delta KCS \backsim \Delta BDS \Rightarrow \dfrac{{KS}}{{BS}} = \dfrac{{SC}}{{SD}} \Rightarrow SB.SC = SK.SD\) (2)
Từ (1) và (2) \( \Rightarrow S{A^2} = SC.SB\)
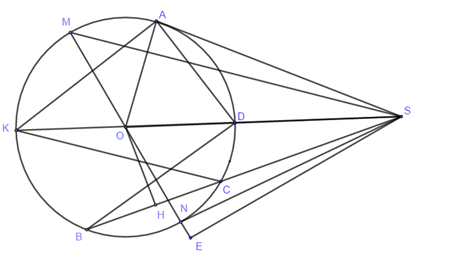
Chọn câu đúng.
Gọi \(D,K\) lần lượt là giao điểm của \(SO\) với đường tròn (\(D\) nằm giữa \(K\) và \(S\))
Xét đường tròn \(\left( O \right)\) có:
\(\angle SAD\) là góc tạo bởi tiếp tuyến và dây cung chắn cung \(AD\)
\(\angle AKS\) là góc nội tiếp chắn cung \(AD\).
Suy ra \(\angle SAD = \angle AKS\).
Xét \(\Delta SDA\) và $\Delta SAK$ có:
\(\angle KSA\) chung
\(\angle SAD = \angle AKS\) (cmt)
\( \Rightarrow \Delta SDA \backsim \Delta SAK \Rightarrow \dfrac{{SA}}{{SK}} = \dfrac{{SD}}{{SA}} \Rightarrow S{A^2} = SK.SD\). (1)
Xét \(\Delta KCS\) và \(\Delta BDS\) ta có:
\(\angle AKC = \angle DBS\) (hai góc nội tiếp cùng chắn cung DC)
\(\angle DSC\) chung
\( \Rightarrow \Delta KCS \backsim \Delta BDS \Rightarrow \dfrac{{KS}}{{BS}} = \dfrac{{SC}}{{SD}} \Rightarrow SB.SC = SK.SD\) (2)
Từ (1) và (2) \( \Rightarrow S{A^2} = SC.SB\)

Đường thẳng qua $O$ vuông góc với \(OM\) cắt các tia \(MC;MD\) lần lượt tại \(E;F\). Xác định hình dạng của tứ giác \(MCOD\) để diện tích tam giác \(MEF\) nhỏ nhất khi \(M\) di động trên tia đối của tia \(BA.\)
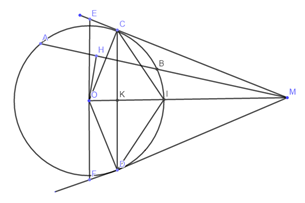
Ta nhận thấy \({S_{MFE}} = 2{S_{MEO}}\) (do có chung đường cao\(MO\)và \(OE = \dfrac{1}{2}FE\))
\( \Rightarrow {S_{MFE}}\max \Leftrightarrow {S_{MEO}}\max \)
Xét \(\Delta MEO\) có: \({S_{MEO}} = \dfrac{1}{2}CO.ME = \dfrac{1}{2}R.\left( {CE + CM} \right)\)
Mà có: \(CM = \dfrac{{CO}}{{\tan \left( {\angle CMO} \right)}} = \dfrac{R}{{\tan \left( {\angle CMO} \right)}};CE = \dfrac{{CO}}{{\tan \left( {\angle CEO} \right)}} = \dfrac{R}{{\tan \left( {{{90}^o} - \angle CMO} \right)}} = \dfrac{R}{{\cot \left( {\angle CMO} \right)}}\)\(\)
\( \Rightarrow {S_{MEO}} = \dfrac{1}{2}{R^2}\left( {\dfrac{1}{{\tan \left( {\angle CMO} \right)}} + \dfrac{1}{{\cot \left( {\angle CMO} \right)}}} \right) = \dfrac{1}{2}{R^2}\left( {\dfrac{1}{{\tan \left( {\angle CMO} \right)}} + \tan \left( {\angle CMO} \right)} \right)\)
Mà có \(\angle CMO\) nhọn (do \(\Delta COM\) vuông tại \(C\)) \( \Rightarrow \tan \left( {\angle CMO} \right) > 0\)
Áp dụng bất đẳng thức cosi ta có :\(\dfrac{1}{{\tan \left( {\angle CMO} \right)}} + \tan \left( {\angle CMO} \right) \ge 2\sqrt {\dfrac{1}{{\tan \left( {\angle CMO} \right)}}.\tan \left( {\angle CMO} \right)} = 2\)
\( \Rightarrow {S_{MFE}} = 2{S_{MEO}} = 2.\dfrac{1}{2}{R^2}\left( {\dfrac{1}{{\tan \left( {\angle CMO} \right)}} + \tan \left( {\angle CMO} \right)} \right) \ge 2{R^2}\)\(\)
Dấu “=” xảy ra khi và chỉ khi \(\dfrac{1}{{\tan \left( {\angle CMO} \right)}} = \tan \left( {\angle CMO} \right) \Leftrightarrow \tan \left( {\angle CMO} \right) = 1 \Leftrightarrow \angle CMO = {45^o}\)
\( \Rightarrow \left\{ \begin{array}{l}CO = CM\\\angle CMD = {90^o}\end{array} \right. \Rightarrow MCOD\) là hình vuông (do có 3 góc vuông và hai cạnh kề nhau bằng nhau).
Chọn câu sai.
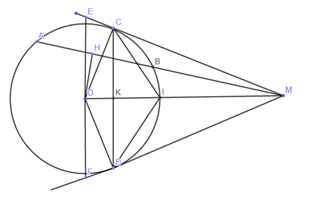
* Xét đường tròn \(\left( {O;R} \right)\) có \(H\) là trung điểm của dây cung \(AB\)\( \Rightarrow OH \bot AB \Rightarrow \angle OHM = {90^o}\) (mối liên hệ giữa đường kính và dây cung)
Xét đường tròn \(\left( {O;R} \right)\) có \(MD\) là tiếp tuyến \( \Rightarrow OD \bot MD \Rightarrow \angle ODM = {90^o}\) (tính chất của tiếp tuyến)
Xét tứ giác \(DOHM\) có: \(\left\{ \begin{array}{l}\angle OHM = {90^o}\\\angle ODM = {90^o}\end{array} \right. \Rightarrow \angle OHM + \angle ODM = {180^o}\)
Suy ra tứ giác \(DOHM\) nội tiếp đường tròn \( \Rightarrow D;O;H;M\) cùng thuộc một đường tròn nên A đúng.
* Xét \(\Delta COM\) và \(\Delta DOM\) có
+)\(OM\) chung
+) \(\angle OCM = \angle ODM = {90^o}\)
+) \(OC = OD = R\)
\( \Rightarrow \Delta COM = \Delta DOM\) (cạnh huyền - cạnh góc vuông) \( \Rightarrow \angle COI = \angle IOD\) (2 góc tương ứng)
\( \Rightarrow CI = ID \Rightarrow \Delta ICD\) cân \( \Rightarrow \angle ICD = \angle IDC\) (Tính chất tam giác cân)
Xét đường tròn \(\left( {O;R} \right)\) có \(\angle ICD\) là góc nội tiếp chắn cung \(ID\); \(\angle IDM\) là góc tạo bởi tiếp tuyến và dây cung chắn cung \(ID\)\( \Rightarrow \angle ICD = \angle IDM\)
Mà có \(\angle ICD = \angle IDC \Rightarrow \angle IDO = \angle IDM\)
\( \Rightarrow ID\) là phân giác \(\angle ODM\) (1)
Chứng minh tương tự có : \(IC\) là phân giác \(\angle MCO\)\(\) (2)
Mà có \(ID\) cắt \(IC\) tại \(I\), suy ra \(I\) là giao điểm của 3 đường phân giác trong \(\Delta MCD\). Suy ra \(I\) là tâm đường tròn nội tiếp \(\Delta MCD\) nên B đúng, C sai.
Chọn câu sai.

* Xét đường tròn \(\left( {O;R} \right)\) có \(H\) là trung điểm của dây cung \(AB\)\( \Rightarrow OH \bot AB \Rightarrow \angle OHM = {90^o}\) (mối liên hệ giữa đường kính và dây cung)
Xét đường tròn \(\left( {O;R} \right)\) có \(MD\) là tiếp tuyến \( \Rightarrow OD \bot MD \Rightarrow \angle ODM = {90^o}\) (tính chất của tiếp tuyến)
Xét tứ giác \(DOHM\) có: \(\left\{ \begin{array}{l}\angle OHM = {90^o}\\\angle ODM = {90^o}\end{array} \right. \Rightarrow \angle OHM + \angle ODM = {180^o}\)
Suy ra tứ giác \(DOHM\) nội tiếp đường tròn \( \Rightarrow D;O;H;M\) cùng thuộc một đường tròn nên A đúng.
* Xét \(\Delta COM\) và \(\Delta DOM\) có
+)\(OM\) chung
+) \(\angle OCM = \angle ODM = {90^o}\)
+) \(OC = OD = R\)
\( \Rightarrow \Delta COM = \Delta DOM\) (cạnh huyền - cạnh góc vuông) \( \Rightarrow \angle COI = \angle IOD\) (2 góc tương ứng)
\( \Rightarrow CI = ID \Rightarrow \Delta ICD\) cân \( \Rightarrow \angle ICD = \angle IDC\) (Tính chất tam giác cân)
Xét đường tròn \(\left( {O;R} \right)\) có \(\angle ICD\) là góc nội tiếp chắn cung \(ID\); \(\angle IDM\) là góc tạo bởi tiếp tuyến và dây cung chắn cung \(ID\)\( \Rightarrow \angle ICD = \angle IDM\)
Mà có \(\angle ICD = \angle IDC \Rightarrow \angle IDO = \angle IDM\)
\( \Rightarrow ID\) là phân giác \(\angle ODM\) (1)
Chứng minh tương tự có : \(IC\) là phân giác \(\angle MCO\)\(\) (2)
Mà có \(ID\) cắt \(IC\) tại \(I\), suy ra \(I\) là giao điểm của 3 đường phân giác trong \(\Delta MCD\). Suy ra \(I\) là tâm đường tròn nội tiếp \(\Delta MCD\) nên B đúng, C sai.
Chọn đẳng thức đúng.
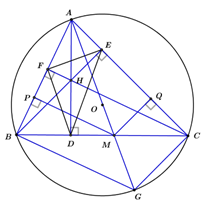
Ta có
\(\begin{array}{l}FH = AH.\sin \widehat {BAD} = AH.\dfrac{{BD}}{{AB}}\\PM = BM.\sin \widehat {ABD} = BM.\dfrac{{AD}}{{AB}}\\ \Rightarrow FH.PM = AH.BM.\dfrac{{BD}}{{AB}}.\dfrac{{AD}}{{AB}}.\end{array}\)\(\)
Chứng minh tương tự ta có:
\(HE.QM = AH.MC.\dfrac{{DC}}{{AC}}.\dfrac{{AD}}{{AC}}\)
Ta có : \(HE.MQ = HF.MP\)
\( \Rightarrow AH.BM.\dfrac{{BD}}{{AB}}.\dfrac{{AD}}{{AB}} = AH.MC.\dfrac{{DC}}{{AC}}.\dfrac{{AD}}{{AC}} \Rightarrow \dfrac{{BM}}{{MC}}.\dfrac{{BD}}{{DC}} = {\left( {\dfrac{{AB}}{{AC}}} \right)^2}\;.\)
Chọn câu đúng.
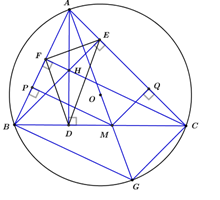
: \(\)
*) Xét tứ giác \(HDCE\) có: \(\left\{ \begin{array}{l}\angle HEC = {90^o}\\\angle HDC = {90^o}\end{array} \right. \Rightarrow \angle HEC + \angle HDC = {180^o}\)
Suy ra tứ giác \(HDCE\) nội tiếp đường tròn \( \Rightarrow \angle HDE = \angle HCE\) ( 2 góc nội tiếp cùng chắn cung \(HE\))
Chứng minh tương tự có \(\angle FBH = \angle FDH\)
Mà có \(\angle FBH = \angle HCE\) (do cùng phụ với \(\angle BAC\))
\( \Rightarrow \angle FDH = \angle HDE\) , suy ra \(HD\) là phân giác \(\angle FDE\)
Chứng minh tương tự ta có : \(HE\)là tia phân giác \(\angle FED\) ; \(FH\) là phân giác \(\angle DFE\)
Suy ra H là giao của 3 đường phân giác trong \(\Delta FDE\) , suy ra H là tâm đường tròn nội tiếp \(\Delta FDE\;\;\left( {dpcm} \right).\)
*) Kéo dài \(AO\) cắt \(\left( O \right)\) tại \(G.\)
Có\(\angle ACG = {90^o}\)(góc nội tiếp chắn nửa đường tròn)
Suy ra \(BH//GC\) (do cùng vuông góc với ${\rm{AC}}$)
Chứng minh tương tự có \(HC//BG\)
\( \Rightarrow BHCG\) là hình bình hành (do có 2 cặp cạnh đối song song)\( \Rightarrow \left\{ \begin{array}{l}BH = GC\\HC = BG\end{array} \right.\)
Xét \(\Delta ACG\) có : \(MQ//GC\) (do cùng vuông góc với ${\rm{AC}}$)
\( \Rightarrow \dfrac{{MQ}}{{GC}} = \dfrac{{AM}}{{AG}}\) (định lí Ta-lét)
Chứng minh tương tự có \(\dfrac{{PM}}{{BG}} = \dfrac{{AM}}{{AG}}\)
\(\)\( \Rightarrow \dfrac{{MQ}}{{GC}} = \dfrac{{PM}}{{BG}}\left( { = \dfrac{{AM}}{{AG}}} \right).\)
Mà có \(\left\{ \begin{array}{l}BH = GC\\HC = BG\end{array} \right. \Rightarrow \dfrac{{MQ}}{{BH}} = \dfrac{{PM}}{{HC}} \Rightarrow \dfrac{{MQ}}{{PM}} = \dfrac{{BH}}{{HC}}\;\;\;\;\;\;\left( 1 \right)\) \(\)
Xét \(\Delta FHB\) và \(\Delta EHC\) có:
\(\angle FBH = \angle HCE\) (do cùng phụ với \(\angle BAC\))
\(\angle BFH = \angle HEC = {90^o}\)
\( \Rightarrow \Delta FHB \backsim \Delta EHC\left( {g - g} \right) \Rightarrow \dfrac{{FH}}{{HE}} = \dfrac{{BH}}{{HC}}\) (2)\(\) \(\)
Từ (1) và (2) \( \Rightarrow \dfrac{{MQ}}{{PM}} = \dfrac{{FH}}{{HE}} \Rightarrow MQ.HE = HF.MP.\)
Vậy cả A, B đều đúng.
Chọn câu đúng.

: \(\)
*) Xét tứ giác \(HDCE\) có: \(\left\{ \begin{array}{l}\angle HEC = {90^o}\\\angle HDC = {90^o}\end{array} \right. \Rightarrow \angle HEC + \angle HDC = {180^o}\)
Suy ra tứ giác \(HDCE\) nội tiếp đường tròn \( \Rightarrow \angle HDE = \angle HCE\) ( 2 góc nội tiếp cùng chắn cung \(HE\))
Chứng minh tương tự có \(\angle FBH = \angle FDH\)
Mà có \(\angle FBH = \angle HCE\) (do cùng phụ với \(\angle BAC\))
\( \Rightarrow \angle FDH = \angle HDE\) , suy ra \(HD\) là phân giác \(\angle FDE\)
Chứng minh tương tự ta có : \(HE\)là tia phân giác \(\angle FED\) ; \(FH\) là phân giác \(\angle DFE\)
Suy ra H là giao của 3 đường phân giác trong \(\Delta FDE\) , suy ra H là tâm đường tròn nội tiếp \(\Delta FDE\;\;\left( {dpcm} \right).\)
*) Kéo dài \(AO\) cắt \(\left( O \right)\) tại \(G.\)
Có\(\angle ACG = {90^o}\)(góc nội tiếp chắn nửa đường tròn)
Suy ra \(BH//GC\) (do cùng vuông góc với ${\rm{AC}}$)
Chứng minh tương tự có \(HC//BG\)
\( \Rightarrow BHCG\) là hình bình hành (do có 2 cặp cạnh đối song song)\( \Rightarrow \left\{ \begin{array}{l}BH = GC\\HC = BG\end{array} \right.\)
Xét \(\Delta ACG\) có : \(MQ//GC\) (do cùng vuông góc với ${\rm{AC}}$)
\( \Rightarrow \dfrac{{MQ}}{{GC}} = \dfrac{{AM}}{{AG}}\) (định lí Ta-lét)
Chứng minh tương tự có \(\dfrac{{PM}}{{BG}} = \dfrac{{AM}}{{AG}}\)
\(\)\( \Rightarrow \dfrac{{MQ}}{{GC}} = \dfrac{{PM}}{{BG}}\left( { = \dfrac{{AM}}{{AG}}} \right).\)
Mà có \(\left\{ \begin{array}{l}BH = GC\\HC = BG\end{array} \right. \Rightarrow \dfrac{{MQ}}{{BH}} = \dfrac{{PM}}{{HC}} \Rightarrow \dfrac{{MQ}}{{PM}} = \dfrac{{BH}}{{HC}}\;\;\;\;\;\;\left( 1 \right)\) \(\)
Xét \(\Delta FHB\) và \(\Delta EHC\) có:
\(\angle FBH = \angle HCE\) (do cùng phụ với \(\angle BAC\))
\(\angle BFH = \angle HEC = {90^o}\)
\( \Rightarrow \Delta FHB \backsim \Delta EHC\left( {g - g} \right) \Rightarrow \dfrac{{FH}}{{HE}} = \dfrac{{BH}}{{HC}}\) (2)\(\) \(\)
Từ (1) và (2) \( \Rightarrow \dfrac{{MQ}}{{PM}} = \dfrac{{FH}}{{HE}} \Rightarrow MQ.HE = HF.MP.\)
Vậy cả A, B đều đúng.
Khi tam giác $ABC$ là tam giác đều. Hãy tính diện tích tam giác $ADE$ theo $R.$
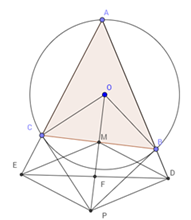
\(\Delta ABC\;\;\)đều, khi đó $A,{\rm{ }}O,{\rm{ }}M,{\rm{ }}F$ thẳng hàng, $AF$ vuông góc với $DE$ tại $F.$\( \Rightarrow \) \({S_{\Delta ADE}}\) $ = \dfrac{1}{2}DE.AF$
\(\Delta ABC\;\;\)đều nên ta có: $\widehat {CAB} = {60^0}$ mà $\widehat {CBP} = \widehat {CAB} = {60^0}$(góc nội tiếp và góc tạo bởi tia tiếp tuyến và dây cung cùng chắn cung BC)
\( \Rightarrow AM = MP;MF = \dfrac{1}{2}MP\)
có \(AB = \;\sqrt {A{M^2} + \;M{B^{2\;}}} \) \( \Rightarrow AB = R\sqrt 3 \)
\(OA = R \Rightarrow AM = \dfrac{3}{2}OA = \dfrac{3}{2}R \Rightarrow AF = \dfrac{3}{2}R + \dfrac{3}{4}R = \dfrac{9}{4}R\)
\(\Delta ABC\;\;\backsim\;\Delta ADE\) \( \Rightarrow \) \(\dfrac{{BC}}{{DE}} = \dfrac{{AM}}{{AF}} = \dfrac{2}{3} \Rightarrow DE = \dfrac{{3\sqrt 3 }}{2}R\)
\( \Rightarrow {S_{\Delta ADE}} = \dfrac{1}{2}DE.AF = \dfrac{{27\sqrt 3 }}{{16}}{R^2}\) .
Đường thẳng \(DE\) đi qua điểm cố định nào ?
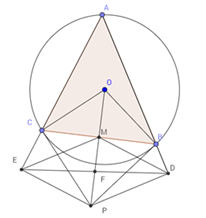
\(\;\widehat {A\;} = \;\widehat {CBP}\;\) cùng chắn cung \(BC\)
Ta có. \(\widehat A\) + \(\widehat {ABC}\) + \(\widehat {ACB} = {180^0}\;\) (tổng ba góc trong tam giác)
Có \(\widehat {CBP}\) + \(\widehat {ABC}\;\)+ \(\widehat {PBD}\) = \({180^0}\) (vì A, B, D thẳng hàng)
\( \Rightarrow \widehat {ACB}\;\)= \(\widehat {PBD}\)
Mà \(\widehat {ACB}\;\) = \(\widehat {MPE}\) (cùng phụ góc $ECM$ )
\(\widehat {PBD}\) = \(\widehat {MPE}\)(cùng chắn cung $BD$ )
=> \(\widehat {MPE}\;\)= \(\widehat {MPE}\)
Mà 2 góc trên ở vị trí so le trong \( \Rightarrow MD//EP\)
Mặt khác ta xét hai tam giác \(\Delta MEP\;;\;\Delta PDM\) ta chứng minh được \(\widehat {EMP} = \;\widehat {MPD}\)
Mà 2 góc lại ở vị trí so le trong nên \(ME//PD\)
Vậy tứ giác $EMDP$ là hình bình hành
\( \Rightarrow ED\) đi qua trung điểm $F$ của $MP$
Vì $B,{\rm{ }}C$ cố định \( \Rightarrow M,P\) cố định \( \Rightarrow \) trung điểm $F$ của $MP$ cố định
Góc \(MEP\) bằng với góc nào dưới đây?
Ta có M là trung điểm của cạnh BC $ \Rightarrow OM \bot BC$ (liên hệ đường kính và dây cung)
Ta có tứ giác BMPD nội tiếp ( vì \(\widehat {BDP}\)+ \(\widehat {BMP}\)=1800) \( \Rightarrow \widehat {MDP}\) = \(\widehat {MBP}\) (tính chất của tứ giác nội tiếp) (1)
Tương tự có tứ giác MCEP nội tiếp => \(\widehat {MEP}\) = \(\widehat {MCP}\) (tính chất của tứ giác nội tiếp) (2)
Mà tiếp tuyến tại B và C cắt nhau tại P nên dễ dàng suy ra được \(\Delta BPC\;\)cân tại P ( tính chất 2 tiếp tuyến cắt nhau)
\( \Rightarrow \widehat {MCP}{\rm{\;}} = \;\widehat {MBP}\;\left( 3 \right)\)
Từ (1); (2);(3) => \(\widehat {MEP}\) = \(\widehat {MDP}\)

Góc \(MEP\) bằng với góc nào dưới đây?
Ta có M là trung điểm của cạnh BC $ \Rightarrow OM \bot BC$ (liên hệ đường kính và dây cung)
Ta có tứ giác BMPD nội tiếp ( vì \(\widehat {BDP}\)+ \(\widehat {BMP}\)=1800) \( \Rightarrow \widehat {MDP}\) = \(\widehat {MBP}\) (tính chất của tứ giác nội tiếp) (1)
Tương tự có tứ giác MCEP nội tiếp => \(\widehat {MEP}\) = \(\widehat {MCP}\) (tính chất của tứ giác nội tiếp) (2)
Mà tiếp tuyến tại B và C cắt nhau tại P nên dễ dàng suy ra được \(\Delta BPC\;\)cân tại P ( tính chất 2 tiếp tuyến cắt nhau)
\( \Rightarrow \widehat {MCP}{\rm{\;}} = \;\widehat {MBP}\;\left( 3 \right)\)
Từ (1); (2);(3) => \(\widehat {MEP}\) = \(\widehat {MDP}\)

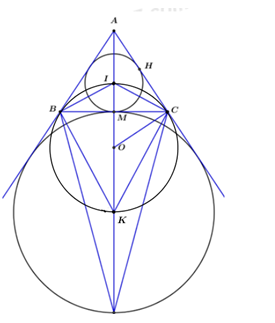
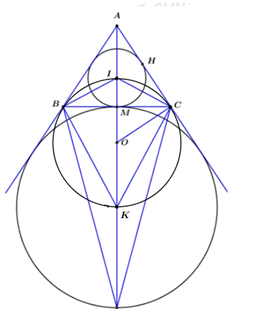
Cho tam giác ABC cân tại A. Gọi I là tâm đường tròn nội tiếp tam giác, K là tâm đường tròn bàng tiếp góc A và O là trung điểm của IK.
Chọn câu đúng.

+) Vì I là tâm đường tròn ngoại tiếp tam giác ABC nên IC là phân giác trong của góc C.
Vì K là tâm đường tròn ngoại tiếp tam giác ABC của góc A nên CK là phân giác ngoài của góc C.
Theo tính chất phân giác trong và phân giác ngoài ta có IC vuông CK nên $\widehat {ICK} = {90^0}$
Chứng minh hoàn toàn tương tự ta có: $\widehat {IBK} = {90^0}$
Xét tứ giác BICK ta có: \(\widehat {IBK} + \widehat {ICK} = {90^0} + {90^0} = {180^0}.\)
\( \Rightarrow BICK\) là tứ giác nội tiếp (tứ giác có tổng hai góc đối diện bằng \({180^0}\))
Do O là trung điểm của IK nên theo tính chất trung tuyến ứng với cạnh huyền bằng nửa cạnh huyền thì OC = OI = OK.
Vậy O là tâm đường tròn ngoại tiếp tứ giác IBKC hay bốn điểm B, I, C, K cùng thuộc (O)
+) Ta có : Tam giác IOC cân tại O nên : $\widehat {OIC} = \widehat {OCI}.$
Mặt khác, theo tính chất góc ngoài của tam giác ta có :
$\widehat {OIC} = \widehat {IAC} + \widehat {ACI} = \dfrac{1}{2}\widehat {BAC} + \dfrac{1}{2}\widehat {ACB} = \dfrac{1}{2}\widehat {BAC} + \dfrac{1}{2}\widehat {ABC}$
$ \Rightarrow \widehat {ICO} + \widehat {ICA} = \dfrac{1}{2}\widehat {BAC} + \dfrac{1}{2}\widehat {ABC} + \dfrac{1}{2}\widehat {ACB} = \dfrac{1}{2}{.180^0} = {90^0}$
$ \Rightarrow OC \bot CA.$
Do đó AC là tiếp tuyến của (O) tại C.
Cả A, B đều đúng.
Cho tam giác ABC cân tại A. Gọi I là tâm đường tròn nội tiếp tam giác, K là tâm đường tròn bàng tiếp góc A và O là trung điểm của IK.
Tính tổng diện tích các hình viên phân giới hạn bởi các cung nhỏ $CI,{\rm{ }}IB,{\rm{ }}BK,{\rm{ }}KC$ và các dây cung tương ứng của $\left( O \right)$ biết $AB = 20,{\rm{ }}BC = 24.$

Gọi diện tích hình cần tính là S, diện tích hình tròn (O) là \(S'\) , gọi giao điểm $BC$ và $IK$ là $M.$
Ta có ngay :
$\begin{array}{l}S = S' - {S_{ICKB}} = \pi I{O^2} - {S_{IBK}} - {S_{IKC}}\\ = \pi \dfrac{{I{K^2}}}{4} - \dfrac{{BM.IK}}{2} - \dfrac{{CM.IK}}{2}\\ = \pi \dfrac{{I{K^2}}}{4} - \dfrac{{BC.IK}}{2}.\end{array}$
Ta có :
\(\begin{array}{l}\;\;\;\;\;{S_{ABC}} = \dfrac{1}{2}AM.BC = \dfrac{{AB + BC + CA}}{2}.IM\\ \Leftrightarrow \sqrt {A{B^2} - B{M^2}} .24 = \left( {AB + BC + CA} \right).IM\\ \Leftrightarrow \sqrt {{{20}^2} - {{\left( {\dfrac{{24}}{2}} \right)}^2}} .24 = \left( {20.2 + 24} \right).IM\\ \Leftrightarrow IM = 6.\end{array}\)
Áp dụng hệ thức lượng trong tam giác \(IBM\) vuông tại \(B\) có đường cao \(BM\) ta có :
\(\begin{array}{l}B{M^2} = IM.MK \Leftrightarrow MK = \dfrac{{B{M^2}}}{{IM}} = \dfrac{{{{12}^2}}}{6} = 24.\\ \Rightarrow IM = IM + MK = 6 + 24 = 30.\\ \Rightarrow S = \dfrac{1}{4}\pi I{K^2} - \dfrac{1}{2}BC.IK = \dfrac{1}{4}\pi {.30^2} - \dfrac{1}{2}.24.30\\ = 225\pi - 360\;\;\left( {dvdt} \right).\end{array}\)
Chọn câu đúng.

+) Vì I là tâm đường tròn ngoại tiếp tam giác ABC nên IC là phân giác trong của góc C.
Vì K là tâm đường tròn ngoại tiếp tam giác ABC của góc A nên CK là phân giác ngoài của góc C.
Theo tính chất phân giác trong và phân giác ngoài ta có IC vuông CK nên $\widehat {ICK} = {90^0}$
Chứng minh hoàn toàn tương tự ta có: $\widehat {IBK} = {90^0}$
Xét tứ giác BICK ta có: \(\widehat {IBK} + \widehat {ICK} = {90^0} + {90^0} = {180^0}.\)
\( \Rightarrow BICK\) là tứ giác nội tiếp (tứ giác có tổng hai góc đối diện bằng \({180^0}\))
Do O là trung điểm của IK nên theo tính chất trung tuyến ứng với cạnh huyền bằng nửa cạnh huyền thì OC = OI = OK.
Vậy O là tâm đường tròn ngoại tiếp tứ giác IBKC hay bốn điểm B, I, C, K cùng thuộc (O)
+) Ta có : Tam giác IOC cân tại O nên : $\widehat {OIC} = \widehat {OCI}.$
Mặt khác, theo tính chất góc ngoài của tam giác ta có :
$\widehat {OIC} = \widehat {IAC} + \widehat {ACI} = \dfrac{1}{2}\widehat {BAC} + \dfrac{1}{2}\widehat {ACB} = \dfrac{1}{2}\widehat {BAC} + \dfrac{1}{2}\widehat {ABC}$
$ \Rightarrow \widehat {ICO} + \widehat {ICA} = \dfrac{1}{2}\widehat {BAC} + \dfrac{1}{2}\widehat {ABC} + \dfrac{1}{2}\widehat {ACB} = \dfrac{1}{2}{.180^0} = {90^0}$
$ \Rightarrow OC \bot CA.$
Do đó AC là tiếp tuyến của (O) tại C.
Cả A, B đều đúng.

