Đường thẳng qua $O$ vuông góc với \(OM\) cắt các tia \(MC;MD\) lần lượt tại \(E;F\). Xác định hình dạng của tứ giác \(MCOD\) để diện tích tam giác \(MEF\) nhỏ nhất khi \(M\) di động trên tia đối của tia \(BA.\)

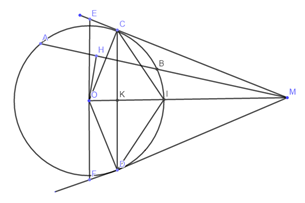
Ta nhận thấy \({S_{MFE}} = 2{S_{MEO}}\) (do có chung đường cao\(MO\)và \(OE = \dfrac{1}{2}FE\))

\( \Rightarrow {S_{MFE}}\max  \Leftrightarrow {S_{MEO}}\max \)

Xét \(\Delta MEO\) có: \({S_{MEO}} = \dfrac{1}{2}CO.ME = \dfrac{1}{2}R.\left( {CE + CM} \right)\)

Mà có: \(CM = \dfrac{{CO}}{{\tan \left( {\angle CMO} \right)}} = \dfrac{R}{{\tan \left( {\angle CMO} \right)}};CE = \dfrac{{CO}}{{\tan \left( {\angle CEO} \right)}} = \dfrac{R}{{\tan \left( {{{90}^o} - \angle CMO} \right)}} = \dfrac{R}{{\cot \left( {\angle CMO} \right)}}\)\(\)

\( \Rightarrow {S_{MEO}} = \dfrac{1}{2}{R^2}\left( {\dfrac{1}{{\tan \left( {\angle CMO} \right)}} + \dfrac{1}{{\cot \left( {\angle CMO} \right)}}} \right) = \dfrac{1}{2}{R^2}\left( {\dfrac{1}{{\tan \left( {\angle CMO} \right)}} + \tan \left( {\angle CMO} \right)} \right)\)

Mà có \(\angle CMO\) nhọn (do \(\Delta COM\) vuông tại \(C\)) \( \Rightarrow \tan \left( {\angle CMO} \right) > 0\)

Áp dụng bất đẳng thức cosi ta có :\(\dfrac{1}{{\tan \left( {\angle CMO} \right)}} + \tan \left( {\angle CMO} \right) \ge 2\sqrt {\dfrac{1}{{\tan \left( {\angle CMO} \right)}}.\tan \left( {\angle CMO} \right)}  = 2\)

\( \Rightarrow {S_{MFE}} = 2{S_{MEO}} = 2.\dfrac{1}{2}{R^2}\left( {\dfrac{1}{{\tan \left( {\angle CMO} \right)}} + \tan \left( {\angle CMO} \right)} \right) \ge 2{R^2}\)\(\)

Dấu “=” xảy ra khi và chỉ khi \(\dfrac{1}{{\tan \left( {\angle CMO} \right)}} = \tan \left( {\angle CMO} \right) \Leftrightarrow \tan \left( {\angle CMO} \right) = 1 \Leftrightarrow \angle CMO = {45^o}\)

\( \Rightarrow \left\{ \begin{array}{l}CO = CM\\\angle CMD = {90^o}\end{array} \right. \Rightarrow MCOD\) là hình vuông (do có 3 góc vuông và hai cạnh kề nhau bằng nhau).