Chọn câu đúng.

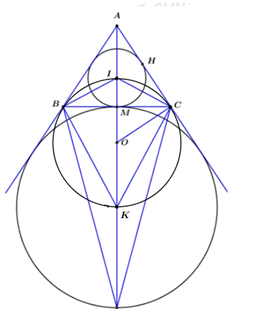
+) Vì I là tâm đường tròn ngoại tiếp tam giác ABC nên IC là phân giác trong của góc C.

Vì K là tâm đường tròn ngoại tiếp tam giác ABC của góc A nên  CK là phân giác ngoài của góc C.

Theo tính chất phân giác trong và phân giác ngoài ta có IC vuông CK nên $\widehat {ICK} = {90^0}$

Chứng minh hoàn toàn tương tự ta có: $\widehat {IBK} = {90^0}$

Xét tứ giác BICK ta có: $\widehat {IBK} + \widehat {ICK} = {90^0} + {90^0} = {180^0}.$

$\Rightarrow BICK$ là tứ giác nội tiếp (tứ giác có tổng hai góc đối diện bằng ${180^0}$)

Do O là trung điểm của IK nên theo tính chất trung tuyến ứng với cạnh huyền bằng nửa cạnh huyền thì OC = OI = OK.

Vậy O là tâm đường tròn ngoại tiếp tứ giác IBKC hay bốn điểm B, I, C, K cùng thuộc (O)

+) Ta có : Tam giác IOC cân tại O nên : $\widehat {OIC} = \widehat {OCI}.$

Mặt khác, theo tính chất góc ngoài của tam giác ta có :

$\widehat {OIC} = \widehat {IAC} + \widehat {ACI} = \dfrac{1}{2}\widehat {BAC} + \dfrac{1}{2}\widehat {ACB} = \dfrac{1}{2}\widehat {BAC} + \dfrac{1}{2}\widehat {ABC}$

$\Rightarrow \widehat {ICO} + \widehat {ICA} = \dfrac{1}{2}\widehat {BAC} + \dfrac{1}{2}\widehat {ABC} + \dfrac{1}{2}\widehat {ACB} = \dfrac{1}{2}{.180^0} = {90^0}$

$\Rightarrow OC \bot CA.$

Do đó AC là tiếp tuyến của (O) tại C.

Cả A, B đều đúng.