Lấy điểm \(N\) thuộc đoạn thẳng \(AB\)( \(N\) khác \(A\), \(N\) khác \(B\)). Lấy điểm \(P\) thuộc tia đối của \(MB\) sao cho \(MP = AN\). Tam tam giác \(CPN\) là tam giác gì? Đường thẳng \(AM\) đi qua trung điểm của đoạn thẳng nào?
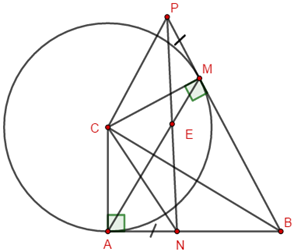
Xét tam giác \(CAN\) và tam giác \(CMP\) có:
\(AN = MP\,\,\,\,\left( {gt} \right)\)
\(\angle CAN = \angle CMP = {90^0}\)
\(AC = CM\)(\(A,M\) cùng thuộc đường tròn \(\left( {C;\,\,CA} \right)\))
\( \Rightarrow \Delta CAN = \Delta CMP\,\,\,\left( {c - g - c} \right)\)
\( \Rightarrow CN = CP\)(2 cạnh tương ứng bằng nhau).
\( \Rightarrow \Delta CNP\) cân tại \(C\).
Gọi \(E\) là giao điểm của \(AM\) và \(PN\).
Vì \(\Delta CAN = \Delta CMP\,\,\,\left( {cmt} \right)\) nên:
\(\angle ACN = \angle MCP\)(2 góc tương ứng bằng nhau)
\( \Rightarrow \angle ACM = \angle ACN + \angle NCM\) \( = \angle PCM + \angle MCN = \angle NCP\)
\( \Rightarrow \)\(\Delta ACM\) và \(\Delta CNP\) là hai tam giác cân đỉnh \(C\) có \(\angle ACM = \angle PCN\)
\( \Rightarrow \angle CNP = \angle CAM\) (các góc ở đáy của các tam giác cân có góc ở đỉnh bằng nhau)
Hay \(\angle CAE = \angle CNE\)
\( \Rightarrow CANE\) là tứ giác nội tiếp. (tứ giác có hai đỉnh kề 1 cạnh cùng nhìn cạnh đối diện dưới các góc bằng nhau).
\( \Rightarrow \angle CEN = {90^0} \Rightarrow CE \bot PN\)
Mà \(\Delta CNP\) cân tại \(C\) (cmt)
\( \Rightarrow CE\) là đường cao, đồng thời là đường trung tuyến của \(\Delta CNP\)
\( \Rightarrow E\) là trung điểm của \(PN\)
Vậy đường thẳng \(AM\) đi qua trung điểm của đoạn thẳng \(NP\).
Chọn khẳng định đúng:
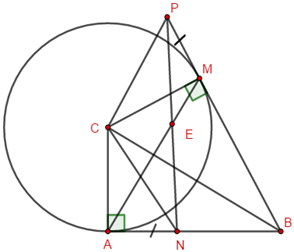
Ta có: tam giác \(ABC\) vuông tại \(A\) nên \(\angle BAC = {90^0}\)
\(MB\) là tiếp tuyến của đường tròn \(\left( {C;CA} \right)\) nên \(\angle CMB = {90^0}\) (định nghĩa tiếp tuyến của đường tròn)
Xét tứ giác \(ACMB\) ta có: \(\angle CAB + \angle CMB = {90^0} + {90^0} = {180^0}\)
\( \Rightarrow ACMB\) là tứ giác nội tiếp đường tròn đường kính BC (tứ giác có tổng hai góc đối diện bằng \({180^0}\)).
Hay bốn điểm \(A,C,M\) và \(B\) cùng thuộc đường tròn đường kính \(BC\).
Khi đó mệnh đề đúng là
Ta có \(\widehat {BCE} = \widehat {DCF}\) (hai góc đối đỉnh). Đặt \(x = \widehat {BCE} = \widehat {DCF}.\)
Theo tính chất góc ngoài tam giác ta có:
\(\widehat {ABC} = x + {40^0}\,\,\left( 1 \right);\widehat {ADC} = x + {20^0}\,\,\left( 2 \right)\)
Lại có \(\widehat {ABC} + \widehat {ADC} = {180^0}\,\,\left( 3 \right)\) (hai góc đối diện của tứ giác nội tiếp).
Từ \(\left( 1 \right),\,\left( 2 \right)\) và \(\left( 3 \right)\) ta nhận được \(\left( {x + {{40}^0}} \right) + \left( {x + {{20}^0}} \right) = {180^0} \Rightarrow x = {60^0}\) .
Từ \(\left( 1 \right)\) ta có \(\widehat {ABC} = {60^0} + {40^0} = {100^0}\) .
Tứ giác \(AHCK\) là
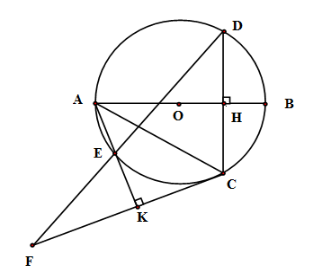
Tứ giác \(AHCK\) có \(\widehat {AHC} = 90^\circ \left( {AB \bot CD} \right);\widehat {AKC} = 90^\circ \left( {AK \bot FC} \right)\) nên \(\widehat {AHC} + \widehat {AKC} = 180^\circ \Rightarrow \) Tứ giác \(AHCK\) nội tiếp.
$\left( I \right):$ Tứ giác \(ABMQ\) nội tiếp; $\left( {II} \right):$ Tứ giác \(ADNP\) nội tiếp. Chọn kết luận đúng.
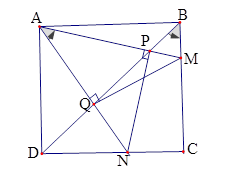
Xét hình vuông \(ABCD\) có \(\widehat {DBC} = \widehat {BDC} = 45^\circ \) (tính chất)
Xét tứ giác \(ABMQ\) có \(\widehat {QAM} = \widehat {QBM} = 45^\circ \) mà hai đỉnh \(A\) và \(B\) cùng nhìn đoạn thẳng \(MQ\) nên \(ABMQ\) là tứ giác nội tiếp.
Xét tứ giác \(APND\) có \(\widehat {PAN} = \widehat {PDN} = 45^\circ \) mà hai đỉnh \(A\) và ${\rm{D}}$ cùng nhìn đoạn thẳng \(PN\) nên \(APND\) là tứ giác nội tiếp.
Số đo góc \(\widehat {BAD}\) là
Ta có \(\widehat {BCE} = \widehat {DCF}\) (hai góc đối đỉnh). Đặt \(x = \widehat {BCE} = \widehat {DCF}.\)
Theo tính chất góc ngoài tam giác ta có:
\(\widehat {ABC} = x + {40^0}\,\,\left( 1 \right);\widehat {ADC} = x + {20^0}\,\,\left( 2 \right)\)
Lại có \(\widehat {ABC} + \widehat {ADC} = {180^0}\,\,\left( 3 \right)\) (hai góc đối diện của tứ giác nội tiếp).
Từ \(\left( 1 \right),\,\left( 2 \right)\) và \(\left( 3 \right)\) ta nhận được \(\left( {x + {{40}^0}} \right) + \left( {x + {{20}^0}} \right) = {180^0} \Rightarrow x = {60^0} \Rightarrow \widehat {BCE} = 60^\circ \) .
Do \(\widehat {BCD},\,\widehat {BCE}\) là hai góc kề bù nên
\(\widehat {BCD} + \,\widehat {BCE} = {180^0} \Rightarrow \widehat {BCD} = {180^0} - {60^0} = {120^0}\)
Ta lại có \(\widehat {BAD},\,\widehat {BCD}\) là hai góc đối diện của tứ giác nội tiếp nên
$\widehat {BAD} + \,\widehat {BCD} = {180^0} \Rightarrow \widehat {BAD} = {180^0} - {120^0} = {60^0}$
Cách khác:
Xét tam giác \(ADE\), theo định lý về tổng ba góc trong tam giác, ta có:
\(\widehat {BAD} + \widehat {CDA} + \widehat {AED} = {180^0}\)
\(\begin{array}{l}
\Rightarrow \widehat {BAD} + \widehat {CDA} + {40^0} = {180^0}\\
\Rightarrow \widehat {BAD} + \widehat {CDA} = {140^0}\,(1*)
\end{array}\)
Xét tam giác \(ABF\), theo định lý về tổng ba góc trong tam giác, ta có:
\(\begin{array}{l}
\widehat {BAD} + \widehat {CBA} + \widehat {AFB} = {180^0}\\
\Rightarrow \widehat {BAD} + \widehat {CBA} + {20^0} = {180^0}\\
\Rightarrow \widehat {BAD} + \widehat {CBA} = {160^0}\,(2*)
\end{array}\)
Vì tứ giác \(ABCD\) nội tiếp đường tròn \((O)\) nên \(\widehat {ADC} + \widehat {CBA} = {180^0}\) (3*) (tổng hai góc đối bằng \(180^0\))
Từ \((1*), (2*)\) và (3*) ta có:
\(\begin{array}{l}
\widehat {BAD} + \widehat {ADC} + \widehat {BAD} + \widehat {CBA} = {140^0} + {160^0}\\
\Rightarrow 2\widehat {BAD} + \left( {\widehat {ADC} + \widehat {CBA}} \right) = {300^0}\\
\Rightarrow 2\widehat {BAD} + {180^0} = {300^0}\\
\Rightarrow 2\widehat {BAD} = {120^0}\\
\Rightarrow \widehat {BAD} = {60^0}
\end{array}\)
Khi đó mệnh đề đúng là
Ta có \(\widehat {BCE} = \widehat {DCF}\) (hai góc đối đỉnh). Đặt \(x = \widehat {BCE} = \widehat {DCF}.\)
Theo tính chất góc ngoài tam giác ta có:
\(\widehat {ABC} = x + {40^0}\,\,\left( 1 \right);\widehat {ADC} = x + {20^0}\,\,\left( 2 \right)\)
Lại có \(\widehat {ABC} + \widehat {ADC} = {180^0}\,\,\left( 3 \right)\) (hai góc đối diện của tứ giác nội tiếp).
Từ \(\left( 1 \right),\,\left( 2 \right)\) và \(\left( 3 \right)\) ta nhận được \(\left( {x + {{40}^0}} \right) + \left( {x + {{20}^0}} \right) = {180^0} \Rightarrow x = {60^0}\) .
Từ \(\left( 1 \right)\) ta có \(\widehat {ABC} = {60^0} + {40^0} = {100^0}\) .
Khi đó mệnh đề đúng là
Ta có \(\widehat {BCE} = \widehat {DCF}\) (hai góc đối đỉnh). Đặt \(x = \widehat {BCE} = \widehat {DCF}.\)
Theo tính chất góc ngoài tam giác ta có:
\(\widehat {ABC} = x + {40^0}\,\,\left( 1 \right);\widehat {ADC} = x + {20^0}\,\,\left( 2 \right)\)
Lại có \(\widehat {ABC} + \widehat {ADC} = {180^0}\,\,\left( 3 \right)\) (hai góc đối diện của tứ giác nội tiếp).
Từ \(\left( 1 \right),\,\left( 2 \right)\) và \(\left( 3 \right)\) ta nhận được \(\left( {x + {{40}^0}} \right) + \left( {x + {{20}^0}} \right) = {180^0} \Rightarrow x = {60^0}\) .
Từ \(\left( 1 \right)\) ta có \(\widehat {ABC} = {60^0} + {40^0} = {100^0}\) .
Tam giác \(ACF\) là tam giác
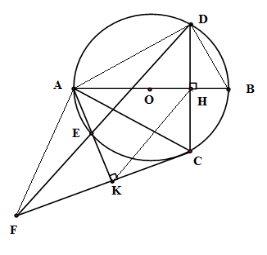
Xét \(\left( O \right)\) có \(\widehat {EAC} = \widehat {EDC}\) (hai góc nội tiếp cùng chắn một cung)
Xét tứ giác nội tiếp \(AHCK\) có \(\widehat {KAC} = \widehat {KHC}\) nên \(\widehat {EDC} = \widehat {KHC}\left( { = \widehat {KAC}} \right)\) mà hai góc ở vị trí đồng vị nên \(KH{\rm{//}}ED\)
Xét tam giác \(CFD\) có \(KH{\rm{//}}ED\)mà \(H\) là trung điểm của \(DC\) ( do \(AB \bot DC\)) nên \(K\) là trung điểm của \(CF\)
Xét tam giác \(ACF\) có \(AK\) vừa là đường trung tuyến vừa là đường cao nên \(\Delta ACF\) cân tại \(A\) .
Tích \(AH.AB\) bằng
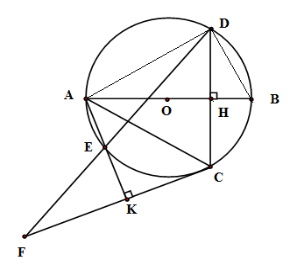
Xét tam giác \(ADB\) có \(\widehat {ADB} = 90^\circ \) (góc nội tiếp chắn nửa đường tròn) \( \Rightarrow \Delta ADB\) vuông tại \(D\)
Do đó \(A{D^2} = AH.AB\) (hệ thức lượng trong tam giác vuông)
Mà \(AD \ne BD;AD < AB\) nên phương án A, B, C sai.
Tứ giác \(AHCK\) là

Tứ giác \(AHCK\) có \(\widehat {AHC} = 90^\circ \left( {AB \bot CD} \right);\widehat {AKC} = 90^\circ \left( {AK \bot FC} \right)\) nên \(\widehat {AHC} + \widehat {AKC} = 180^\circ \Rightarrow \) Tứ giác \(AHCK\) nội tiếp.
Tứ giác \(AHCK\) là

Tứ giác \(AHCK\) có \(\widehat {AHC} = 90^\circ \left( {AB \bot CD} \right);\widehat {AKC} = 90^\circ \left( {AK \bot FC} \right)\) nên \(\widehat {AHC} + \widehat {AKC} = 180^\circ \Rightarrow \) Tứ giác \(AHCK\) nội tiếp.
Năm điểm nào sau đây cùng thuộc một đường tròn?
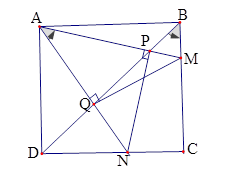
Từ kết quả câu trước ta suy ra \(\widehat {ADP} = \widehat {ANP} = {45^0},\widehat {QAM} = \widehat {QBM} = {45^0}\)\( \Rightarrow NP \bot AM,MQ \bot AN\). Tập hợp các điểm \(P,Q,C\) nhìn đoạn \(MN\) dưới một góc vuông, nên các điểm này nằm trên đường tròn đường kính \(MN\).
$\left( I \right):$ Tứ giác \(ABMQ\) nội tiếp; $\left( {II} \right):$ Tứ giác \(ADNP\) nội tiếp. Chọn kết luận đúng.

Xét hình vuông \(ABCD\) có \(\widehat {DBC} = \widehat {BDC} = 45^\circ \) (tính chất)
Xét tứ giác \(ABMQ\) có \(\widehat {QAM} = \widehat {QBM} = 45^\circ \) mà hai đỉnh \(A\) và \(B\) cùng nhìn đoạn thẳng \(MQ\) nên \(ABMQ\) là tứ giác nội tiếp.
Xét tứ giác \(APND\) có \(\widehat {PAN} = \widehat {PDN} = 45^\circ \) mà hai đỉnh \(A\) và ${\rm{D}}$ cùng nhìn đoạn thẳng \(PN\) nên \(APND\) là tứ giác nội tiếp.
$\left( I \right):$ Tứ giác \(ABMQ\) nội tiếp; $\left( {II} \right):$ Tứ giác \(ADNP\) nội tiếp. Chọn kết luận đúng.

Xét hình vuông \(ABCD\) có \(\widehat {DBC} = \widehat {BDC} = 45^\circ \) (tính chất)
Xét tứ giác \(ABMQ\) có \(\widehat {QAM} = \widehat {QBM} = 45^\circ \) mà hai đỉnh \(A\) và \(B\) cùng nhìn đoạn thẳng \(MQ\) nên \(ABMQ\) là tứ giác nội tiếp.
Xét tứ giác \(APND\) có \(\widehat {PAN} = \widehat {PDN} = 45^\circ \) mà hai đỉnh \(A\) và ${\rm{D}}$ cùng nhìn đoạn thẳng \(PN\) nên \(APND\) là tứ giác nội tiếp.
Cho tứ giác ABCD nội tiếp. Chọn câu sai:
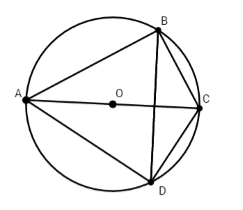
+) $\widehat {BAD} + \widehat {BCD} = {180^ \circ }$(tổng hai góc đối)
+) $\widehat {ABD} = \widehat {ACD}$ (hai góc nội tiếp cùng chắn cung AD)
+)$\widehat A + \widehat B + \widehat C + \widehat D = {360^0}$(tổng 4 góc trong tứ giác).
Cho tứ giác ABCD có số đo các góc A, B, C, D lần lượt như sau. Trường hợp nào thì tứ giác ABCD có thể là tứ giác nội tiếp.
Xét các đáp án ta có:
+) Đáp án A: \(\left\{ \begin{array}{l}\widehat A + \widehat C = {50^0} + {130^0} = {180^0}\\\widehat B + \widehat D = {60^0} + {140^0} = {200^0}\end{array} \right. \Rightarrow \) loại đáp án A.
+) Đáp án B: \(\left\{ \begin{array}{l}\widehat A + \widehat C = {65^0} + {115^0} = {180^0}\\\widehat B + \widehat D = {85^0} + {95^0} = {180^0}\end{array} \right. \Rightarrow \) đáp án B đúng.
+) Đáp án C: \(\left\{ \begin{array}{l}\widehat A + \widehat C = {82^0} + {98^0} = {180^0}\\\widehat B + \widehat D = {90^0} + {100^0} = {190^0}\end{array} \right. \Rightarrow \) loại đáp án C.
Cho tam giác ABC vuông tại A đường cao AH. Kẻ HE vuông góc với AB taị E. kẻ HF vuông góc với AC tại F. Chọn câu đúng:
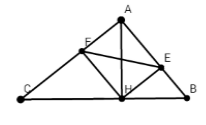
Xét tứ giác AEHF có:
\(\widehat A = \widehat E = \widehat F = {90^0}\)
\( \Rightarrow \)Tứ giác AEHF là hình chữ nhật (dhnb).
\( \Rightarrow \) Tứ giác AEHF là tứ giác nội tiếp (có tổng hai góc đối diện bằng \({180^0}\))
$ \Rightarrow \widehat {{\rm{AF}}E} = \widehat {AHE}$ (hai góc cùng nhìn đoạn AE).
$\widehat {{\rm{AHE}}} = \widehat {ABH}$ (cùng phụ $\widehat {{\rm{BHE}}}$)
$ \Rightarrow \widehat {{\rm{AF}}E} = \widehat {ABC}\;\;\;\left( { = \widehat {AHE}} \right)$.
Xét tứ giác BEFC có: \(\widehat {AFE}\) là góc ngoài tại đỉnh \(F\) và \(\widehat {AFE} = \widehat {ABC}\;\;\;\left( {cmt} \right).\)
$ \Rightarrow $BEFC nội tiếp (dấu hiệu nhận biết).
Tứ giác $ABCD$ nội tiếp đường tròn có hai cạnh đối $AB$ và $CD$ cắt nhau tại $M$ và $\widehat {BAD} = {80^0}$ thì $\widehat {BCM} = ?$
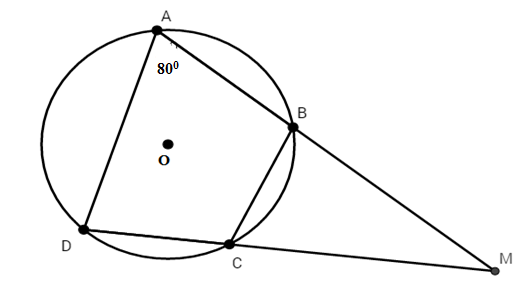
Tứ giác $ABCD$ nội tiếp nên có: $\widehat {DAB} + \widehat {BCD} = {180^0}$$ \Rightarrow \widehat {BCD} = {180^0} - {80^0} = {100^0}$
Mà $\widehat {BCD} + \widehat {BCM} = {180^0}$(kề bù) $ \Rightarrow \widehat {BCM} = {180^0} - {100^0} = {80^0}$
Cho điểm A nằm ngoài đường tròn (O) qua A kẻ hai tiếp tuyến AB và AC với đường tròn (B, C là tiếp điểm) . Chọn đáp án đúng:
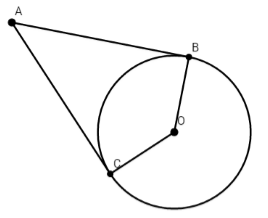
Ta có AB và AC là hai tiếp tuyến cắt nhau
\( \Rightarrow AB = AC\) (tính chất hai tiếp tuyến cắt nhau)
Xét tứ giác ABOC có: $\left\{ \begin{array}{l}AB = AC\;\;\left( {cmt} \right)\\OB = OC\;\;\;\left( { = R} \right)\end{array} \right.$
$ \Rightarrow $ tứ giác ABOC chưa là hình thoi và không là hình bình hành.
$ \Rightarrow $đáp án A, D sai.
Có $\widehat {{\rm{ABO}}} = {90^0}$(do AB là tiếp tuyến của (O))
$\widehat {{\rm{ACO}}} = {90^0}$(do AC là tiếp tuyến của (O))
$ \Rightarrow \widehat {{\rm{ABO}}} + \widehat {ACO} = {180^0}$ $ \Rightarrow $tứ giác ABOC nội tiếp (dhnb).
\( \Rightarrow \) đáp án B đúng.

