Câu hỏi:
2 năm trước
Lấy điểm \(N\) thuộc đoạn thẳng \(AB\)( \(N\) khác \(A\), \(N\) khác \(B\)). Lấy điểm \(P\) thuộc tia đối của \(MB\) sao cho \(MP = AN\). Tam tam giác \(CPN\) là tam giác gì? Đường thẳng \(AM\) đi qua trung điểm của đoạn thẳng nào?
Trả lời bởi giáo viên
Đáp án đúng: b
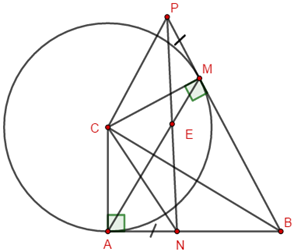
Xét tam giác \(CAN\) và tam giác \(CMP\) có:
\(AN = MP\,\,\,\,\left( {gt} \right)\)
\(\angle CAN = \angle CMP = {90^0}\)
\(AC = CM\)(\(A,M\) cùng thuộc đường tròn \(\left( {C;\,\,CA} \right)\))
\( \Rightarrow \Delta CAN = \Delta CMP\,\,\,\left( {c - g - c} \right)\)
\( \Rightarrow CN = CP\)(2 cạnh tương ứng bằng nhau).
\( \Rightarrow \Delta CNP\) cân tại \(C\).
Gọi \(E\) là giao điểm của \(AM\) và \(PN\).
Vì \(\Delta CAN = \Delta CMP\,\,\,\left( {cmt} \right)\) nên:
\(\angle ACN = \angle MCP\)(2 góc tương ứng bằng nhau)
\( \Rightarrow \angle ACM = \angle ACN + \angle NCM\) \( = \angle PCM + \angle MCN = \angle NCP\)
\( \Rightarrow \)\(\Delta ACM\) và \(\Delta CNP\) là hai tam giác cân đỉnh \(C\) có \(\angle ACM = \angle PCN\)
\( \Rightarrow \angle CNP = \angle CAM\) (các góc ở đáy của các tam giác cân có góc ở đỉnh bằng nhau)
Hay \(\angle CAE = \angle CNE\)
\( \Rightarrow CANE\) là tứ giác nội tiếp. (tứ giác có hai đỉnh kề 1 cạnh cùng nhìn cạnh đối diện dưới các góc bằng nhau).
\( \Rightarrow \angle CEN = {90^0} \Rightarrow CE \bot PN\)
Mà \(\Delta CNP\) cân tại \(C\) (cmt)
\( \Rightarrow CE\) là đường cao, đồng thời là đường trung tuyến của \(\Delta CNP\)
\( \Rightarrow E\) là trung điểm của \(PN\)
Vậy đường thẳng \(AM\) đi qua trung điểm của đoạn thẳng \(NP\).
Hướng dẫn giải:
Chứng minh \(CN = CP\)(2 cạnh tương ứng bằng nhau).
\( \Rightarrow \Delta CNP\) cân tại \(C\).
Chứng minh \(CE\) là đường cao, đồng thời là đường trung tuyến của \(\Delta CNP\)\( \Rightarrow E\) là trung điểm của \(PN\)
