Số đo góc \(\widehat {BAD}\) là
Ta có \(\widehat {BCE} = \widehat {DCF}\) (hai góc đối đỉnh).
Đặt \(x = \widehat {BCE} = \widehat {DCF}.\)
Theo tính chất góc ngoài tam giác ta có:
\(\begin{array}{l}\widehat {ABC} = x + {45^0}\,\,\left( 1 \right)\\\widehat {ADC} = x + {25^0}\,\,\left( 2 \right)\end{array}\)
Lại có \(\widehat {ABC} + \widehat {ADC} = {180^0}\,\,\left( 3 \right)\) (hai góc đối diện của tứ giác nội tiếp).
Từ \(\left( 1 \right),\,\left( 2 \right)\) và \(\left( 3 \right)\) ta nhận được
\(\left( {x + {{45}^0}} \right) + \left( {x + {{25}^0}} \right) = {180^0} \Rightarrow x = {55^0} \Rightarrow \widehat {BCE} = {55^0}.\)
Do \(\widehat {BCD},\,\widehat {BCE}\) là hai góc kề bù nên
\(\widehat {BCD} + \,\widehat {BCE} = {180^0} \Rightarrow \widehat {BCD} = {180^0} - {55^0} = {125^0}.\)
Ta lại có \(\widehat {BAD},\,\widehat {BCD}\) là hai góc đối diện của tứ giác nội tiếp nên
$\widehat {BAD} + \,\widehat {BCD} = {180^0} \Rightarrow \widehat {BAD} = {180^0} - {125^0} = {55^0}.$
Chọn câu đúng:
Ta có \(\widehat {BCE} = \widehat {DCF}\) (hai góc đối đỉnh).
Đặt \(x = \widehat {BCE} = \widehat {DCF}.\)
Theo tính chất góc ngoài tam giác ta có:
\(\begin{array}{l}\widehat {ABC} = x + {45^0}\,\,\left( 1 \right)\\\widehat {ADC} = x + {25^0}\,\,\left( 2 \right)\end{array}\)
Lại có \(\widehat {ABC} + \widehat {ADC} = {180^0}\,\,\left( 3 \right)\) (hai góc đối diện của tứ giác nội tiếp).
Từ \(\left( 1 \right),\,\left( 2 \right)\) và \(\left( 3 \right)\) ta nhận được
\(\left( {x + {{45}^0}} \right) + \left( {x + {{25}^0}} \right) = {180^0} \Rightarrow x = {55^0}.\)
Từ \(\left( 1 \right)\) ta có \(\widehat {ABC} = {55^0} + {45^0} = {100^0}.\)
Chọn câu đúng:
Ta có \(\widehat {BCE} = \widehat {DCF}\) (hai góc đối đỉnh).
Đặt \(x = \widehat {BCE} = \widehat {DCF}.\)
Theo tính chất góc ngoài tam giác ta có:
\(\begin{array}{l}\widehat {ABC} = x + {45^0}\,\,\left( 1 \right)\\\widehat {ADC} = x + {25^0}\,\,\left( 2 \right)\end{array}\)
Lại có \(\widehat {ABC} + \widehat {ADC} = {180^0}\,\,\left( 3 \right)\) (hai góc đối diện của tứ giác nội tiếp).
Từ \(\left( 1 \right),\,\left( 2 \right)\) và \(\left( 3 \right)\) ta nhận được
\(\left( {x + {{45}^0}} \right) + \left( {x + {{25}^0}} \right) = {180^0} \Rightarrow x = {55^0}.\)
Từ \(\left( 1 \right)\) ta có \(\widehat {ABC} = {55^0} + {45^0} = {100^0}.\)
Cho \(\Delta ABC\) cân tại \(A\) có \(\widehat {BAC} = {130^0}.\) Trên nửa mặt phẳng bờ \(BC\) không chứa đỉnh \(A\), kẻ \(Bx \bot BA;Cy \bot CA\), \(Bx\) và \(Cy\) cắt nhau tại D. Chọn đáp án sai.
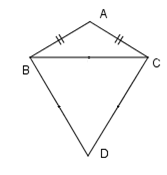
Theo đề bài ta có \(\widehat {ABD} = \widehat {ACD} = 90^\circ \Rightarrow \widehat {ABD} + \widehat {ACD} = 90^\circ + 90^\circ = 180^\circ \) mà hai góc \(\widehat {ABD};\widehat {ACD}\) ở vị trí đối nhau nên tứ giác \(ABDC\) là tứ giác nội tiếp nên đáp án B đúng.
+ Lại có \(\Delta ABC\) cân tại \(A\) có \(\widehat {BAC} = 130^\circ \Rightarrow \widehat {ABC} = \widehat {ACB} = \dfrac{{180^\circ - 130^\circ }}{2} = 25^\circ \)
+ Ta có \(\widehat {BDC} + \widehat {ABC} = 90^\circ \Rightarrow \widehat {BDC} = 90^\circ - 25^\circ = 65^\circ \)
Và \(\widehat {BCD} + \widehat {ACB} = 90^\circ \Rightarrow \widehat {BCD} = 90^\circ - 25^\circ = 65^\circ \)
Từ đó suy ra tam giác \(BCD\) cân tại \(D\) nên đáp án A đúng.
+ Xét tứ giác \(ABDC\) nội tiếp nên \(\widehat {BAC} + \widehat {BDC} = 180^\circ \Leftrightarrow \widehat {BDC} = 180^\circ - \widehat {BAC} = 180^\circ - 130^\circ = 50^\circ \) nên D đúng.
Ta chưa đủ điều kiện để suy ra tứ giác \(ABDC\) là hình thoi nên C sai.
Cho hình bình hành \(ABCD.\) Đường tròn đi qua ba đỉnh \(A,\,B,\,C\) cắt đường thẳng \(CD\) tại \(P\,\,\left( {P \ne C} \right).\) Khi đó
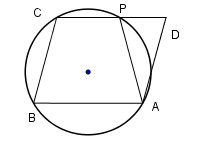
Do tứ giác \(ABCP\) nội tiếp (vì có 4 đỉnh cùng thuộc đường tròn) và \(\widehat {BAP},\,\widehat {BCP}\) là các góc đối nên
\(\widehat {BAP} + \widehat {BCP} = {180^0}\,\,\left( 1 \right).\)
Do \(ABCD\) là hình bình hành nên \(CD//AB\) suy ra
\(\widehat {ABC} + \widehat {BCP} = {180^0}\,\,\left( 2 \right).\)
Từ \(\left( 1 \right)\) và \(\left( 2 \right)\) ta nhận được \(\widehat {BAP} = \widehat {ABC}.\)
Mặt khác \(CP//AB\) nên \(ABCP\) là hình thang cân. Đáp án A đúng.
Từ đó ta suy ra \(AP = BC\,\,\left( 3 \right).\) (Đáp án C đúng)
Do \(BC = AD\) (vì \(ABCD\) là hình bình hành) \(\left( 4 \right)\)
Từ \((3)\) và \(\left( 4 \right)\) ta suy ra \(AP = AD.\) Đáp án B đúng.
Vậy cả ba đáp án \(A,\,\,B,\,\,C\) đều đúng.
Tia phân giác góc \(\widehat {BAD}\) của hình bình hành \(ABCD\) cắt các đường thẳng \(BC\) và \(DC\) lần lượt tại hai điểm \(M\) và \(N.\) Dựng ra phía ngoài hình bình hành \(ABCD\) tam giác cân \(MCO\) với \(\widehat {MOC} = \widehat {BAD}\). Khi đó:
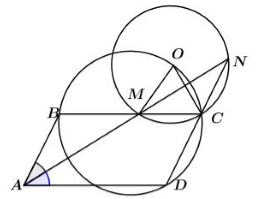
Ta có \(BM//AD\) nên \(\widehat {BMA} = \widehat {MAD}.\)
Mặt khác \(AM\) là phân giác của \(\widehat {BAD}\) nên \(\widehat {BAM} = \widehat {MAD}.\)
Từ đó \(\widehat {BAM} = \widehat {AMB.}\)
Vậy \(\Delta ABM\) cân tại \(B.\) Suy ra \(BM = BA = DC.\)
Tam giác \(OMC\) cân tại \(O\) nên \(OM = OC.\)
Đặt \(\alpha = \widehat {BAD},\) ta có \(\widehat {OCD} = \widehat {BCD} + \widehat {OCM} = \alpha + \dfrac{1}{2}\left( {{{180}^0} - \alpha } \right) = {90^0} + \dfrac{\alpha }{2}\,\,\left( 1 \right).\)
Các góc \(\widehat {BMO},\,\widehat {OMC}\) kề bù nên
\(\widehat {BMO} = {180^0} - \,\widehat {OMC} = {180^0} - \,\widehat {OCM} = {90^0} + \dfrac{\alpha }{2}\,\,\left( 2 \right).\)
Từ \(\left( 1 \right)\) và \(\left( 2 \right)\) suy ra \(\widehat {OCD} = \widehat {BMO}.\)
Xét hai tam giác \(\Delta OBM,\,\Delta ODC\) có \(\left\{ \begin{array}{l}\widehat {OCD} = \widehat {BMO}\\OM = OC\\BM = CD\end{array} \right.\) nên \(\Delta OBM = \Delta ODC\,\,\left( {c.g.c} \right).\)
Do đó \(\widehat {OBM} = \widehat {ODC}.\) Điều này chứng tỏ \(BOCD\) là tứ giác nội tiếp. Do đó bốn điểm \(B,\,O,\,C,\,D\) thuộc cùng một đường tròn.
Cho tam giác nhọn \(ABC\) nội tiếp đường tròn \(\left( O \right),\) các đường cao \(AD,\,BE,\,CF\,\left( {D \in BC,\,E \in AC,\,F \in AB} \right)\) cắt nhau tại \(H\). Khi đó ta có
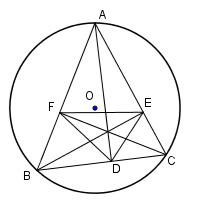
Do \(AD,\,BE\) là các đường cao nên \(\widehat {HDC} = \widehat {HEC} = {90^0}.\)
Do đó $\widehat {HDC} + \widehat {HEC} = {90^0} + {90^0} = {180^0}.$
Vậy tứ giác \(DCEH\) là tứ giác nội tiếp.
Các góc \(\widehat {HED},\,\widehat {HCD}\) cùng chắn cung \(HD\) nên
\(\widehat {HED} = \,\widehat {HCD}\,\,\left( 1 \right).\)
Xét hai tam giác \(\Delta BDE,\,\,\Delta BHC\) có \(\widehat {HED} = \,\widehat {HCD}\,\) (theo \(\left( 1 \right)\) ) và góc \(\widehat {EBC}\) chung.
Do đó \(\Delta BDE \sim \,\Delta BHC.\)Từ đó ta nhận được \(\dfrac{{BD}}{{BH}} = \dfrac{{BE}}{{BC}} \Rightarrow BH.BE = BC.BD.\) Đáp án A đúng.
Chứng minh tương tự ta có \(CH.CF = CD.CB.\) Đáp án B đúng.
Cho tứ giác ABCD nội tiếp (O) . M là điểm chính giữa cung AB. Nối M với D, M với C cắt AB lần lượt ở E và P. Trong các khẳng định sau, khẳng định nào đúng?
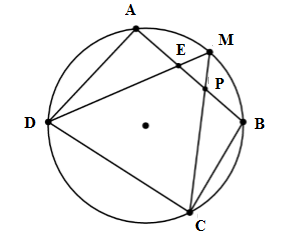
Theo đề bài ta có: M là điểm chính giữa cung AB nên \(\overparen {AM}=\overparen {MB}\)
Xét đường tròn (O) có:
+) \(\widehat {MCD}\) là góc nội tiếp chắn cung $DM \Rightarrow \widehat {MCD} = \dfrac{1}{2}sđ \overparen{DM}.\;\;\left( 1 \right)$
+) \(\widehat {AED}\) là góc có đỉnh nằm trong đường tròn chắn cung \(MB\) và cung \(AD\)
$ \Rightarrow \widehat {MCD} = \dfrac{1}{2}\left( {sđ \overparen{AD} + sđ \overparen{MB}} \right) $$= \dfrac{1}{2}\left( {sđ \overparen{AD} + sđ \overparen{MA}} \right) $$= \dfrac{1}{2}sđ \overparen{DM}\;\;\;\left( 2 \right)$
Từ (1) và (2) $ \Rightarrow \widehat {MCD} = \widehat {AED} $$= \dfrac{1}{2}sđ \overparen{DM}.$
Xét tứ giác DEPC có: \(\widehat {MCD} = \widehat {AED}\;\;\left( {cmt} \right)\)
$ \Rightarrow $PEDC nội tiếp (góc ngoài của một đỉnh bằng góc trong của đỉnh đối diện).
Cho tam giác ABC vuông tại A. Điểm E di động trên cạnh AB. Qua B vẽ một đường thẳng vuông góc cới CE tại D và cắt tia CA tại H. Biết $\widehat {BCA} = {30^0}.$ Số đo $\widehat {ADH}$ là:
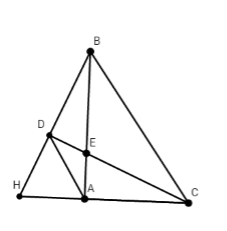
Xét tứ giác ACBD ta có:
$\widehat {BAC} = \widehat {BDC} = {90^0}$ và cùng nhìn đoạn BC.
\( \Rightarrow \) Tứ giác ACBD là tứ giác nội tiếp (dhnb).
$\begin{array}{l} \Rightarrow \widehat {BDA} + \widehat {BCA} = {180^ \circ }\\ \Leftrightarrow \widehat {BDA} = {180^0} - \widehat {BCA} = {180^0} - {30^0} = {150^0}.\end{array}$
Có góc $\widehat {HDA}$ và $\widehat {BDA}$ kề bù nên $\widehat {HDA} = {180^0} - \widehat {BDA} = {30^0}$
Cho tứ giác \(ABCD\) nội tiếp đường tròn \(\left( O \right)\) (hình \(1\) ). Chọn khẳng định đúng nhất?
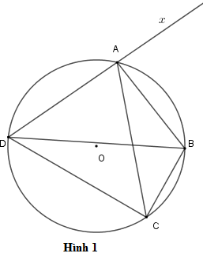
Vì tứ giác \(ABCD\) là tứ giác nội tiếp nên
\(\widehat {BDC} = \widehat {BAC}\) (hai góc nội tiếp cùng chắn cung \(BC\) )
\(\widehat {ABC} + \widehat {ADC} = 180^\circ \) (tổng hai góc đối bằng \(180^\circ \) )
\(\widehat {DCB} = \widehat {BAx}\) (góc ngoài tại một đỉnh bằng góc trong tại đỉnh đối với đỉnh đó)
Phương án A, B, C đúng
Tứ giác ở hình nào dưới đây là tứ giác nội tiếp?
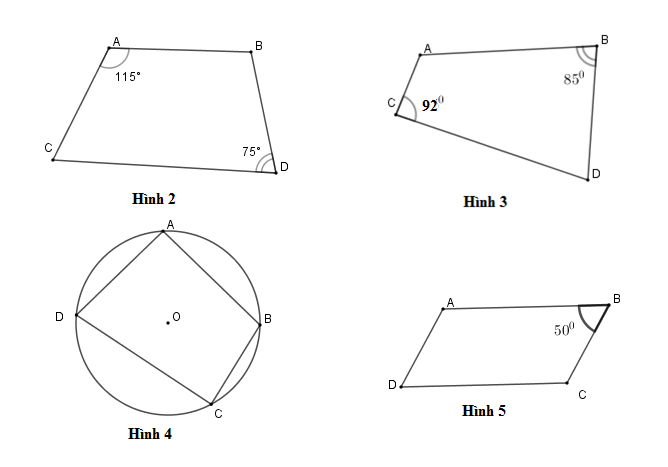
Hình 2 sai vì \(\widehat A + \widehat C = {115^0} + {75^0} = {190^0} \ne {180^0}\) .
Hình 3 sai vì \(\widehat C + \widehat B = {92^0} + {85^0} = {177^0} \ne {180^0}\) .
Hình 5 sai vì \(\widehat D + \widehat B = {50^0} + {50^0} = {100^0} \ne {180^0}\) .
Hình 4 đúng vì tứ giác này có \(4\) đỉnh cùng thuộc một đường tròn.
Cho nửa đường tròn \(\left( {O;R} \right)\) đường kính \(BC.\) Lấy điểm \(A\) trên tia đối của tia \(CB.\) Kẻ tiếp tuyến $AF,Bx$ của nửa đường tròn \(\left( O \right)\) (với \(F\) là tiếp điểm). Tia \(AF\) cắt tia \(Bx\) của nửa đường tròn tại \(D.\) Khi đó tứ giác \(OBDF\) là:
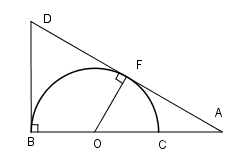
Ta có \(\widehat {DBO} = {90^0}\) và \(\widehat {DFO} = {90^0}\) ( tính chất tiếp tuyến).
Tứ giác \(OBDF\) có \(\widehat {DBO} + \widehat {DFO} = {90^0} + {90^0} = {180^0}\) nên nội tiếp được trong một đường tròn.
Tứ giác $ABCD$ nội tiếp đường tròn có hai cạnh đối $AB$ và $CD$ cắt nhau tại $M$ và $\widehat {BAD} = {70^0}$ thì $\widehat {BCM} = ?$
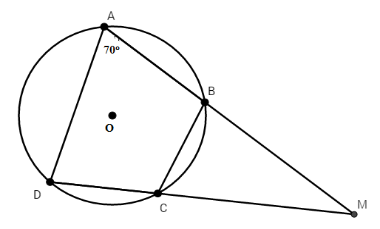
Tứ giác $ABCD$ nội tiếp nên có: $\widehat {DAB} + \widehat {BCD} = {180^0}$$ \Rightarrow \widehat {BCD} = {180^0} - {70^0} = {110^0}$
Mà $\widehat {BCD} + \widehat {BCM} = {180^0}$(kề bù) $ \Rightarrow \widehat {BCM} = {180^0} - {110^0} = {70^0}$
Cho đường tròn $\left( O \right)$ đường kính $AB$ . Gọi $H$ là điểm nằm giữa $O$ và $B$. Kẻ dây $CD$ vuông góc với $AB$ tại $H$ . Trên cung nhỏ $AC$ lấy điểm $E$ kẻ $CK$ vuông góc $AE$ tại $K$ . Đường thẳng $DE$ cắt $CK$ tại $F$. Chọn câu đúng:
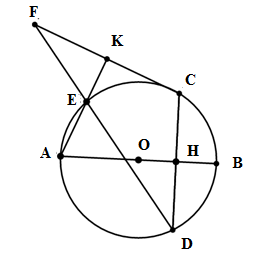
Có $\widehat {AHC} = {90^0}$(CD vuông góc AB); $\widehat {AKC} = {90^0}$ (AK vuông góc CF)
$ \Rightarrow \widehat {{\rm{AHC}}} + \widehat {AKC} = {180^0}$ $ \Rightarrow $ tứ giác AHCK nội tiếp \( \Rightarrow \) phương án A đúng, B sai.
\( \Rightarrow \widehat {EAO} + \widehat {HCK} = {180^0}\) (hai góc đối diện)\( \Rightarrow \) phương án C sai.
Xét tam giác vuông \(ADB\) có \(AH.AB = A{D^2}\) (hệ thức lượng trong tam giác vuông) nên phương án D sai.
Cho hình vẽ dưới đây
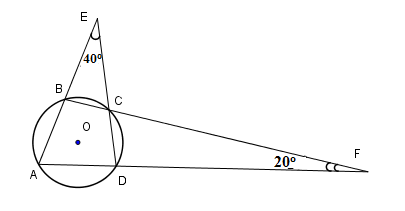
Khi đó mệnh đề đúng là
Ta có \(\widehat {BCE} = \widehat {DCF}\) (hai góc đối đỉnh). Đặt \(x = \widehat {BCE} = \widehat {DCF}.\)
Theo tính chất góc ngoài tam giác ta có:
\(\widehat {ABC} = x + {40^0}\,\,\left( 1 \right);\widehat {ADC} = x + {20^0}\,\,\left( 2 \right)\)
Lại có \(\widehat {ABC} + \widehat {ADC} = {180^0}\,\,\left( 3 \right)\) (hai góc đối diện của tứ giác nội tiếp).
Từ \(\left( 1 \right),\,\left( 2 \right)\) và \(\left( 3 \right)\) ta nhận được \(\left( {x + {{40}^0}} \right) + \left( {x + {{20}^0}} \right) = {180^0} \Rightarrow x = {60^0}\) .
Từ \(\left( 1 \right)\) ta có \(\widehat {ABC} = {60^0} + {40^0} = {100^0}\) .
Cho hình vẽ dưới đây

Số đo góc \(\widehat {BAD}\) là
Ta có \(\widehat {BCE} = \widehat {DCF}\) (hai góc đối đỉnh). Đặt \(x = \widehat {BCE} = \widehat {DCF}.\)
Theo tính chất góc ngoài tam giác ta có:
\(\widehat {ABC} = x + {40^0}\,\,\left( 1 \right);\widehat {ADC} = x + {20^0}\,\,\left( 2 \right)\)
Lại có \(\widehat {ABC} + \widehat {ADC} = {180^0}\,\,\left( 3 \right)\) (hai góc đối diện của tứ giác nội tiếp).
Từ \(\left( 1 \right),\,\left( 2 \right)\) và \(\left( 3 \right)\) ta nhận được \(\left( {x + {{40}^0}} \right) + \left( {x + {{20}^0}} \right) = {180^0} \Rightarrow x = {60^0} \Rightarrow \widehat {BCE} = 60^\circ \) .
Do \(\widehat {BCD},\,\widehat {BCE}\) là hai góc kề bù nên
\(\widehat {BCD} + \,\widehat {BCE} = {180^0} \Rightarrow \widehat {BCD} = {180^0} - {60^0} = {120^0}\)
Ta lại có \(\widehat {BAD},\,\widehat {BCD}\) là hai góc đối diện của tứ giác nội tiếp nên
$\widehat {BAD} + \,\widehat {BCD} = {180^0} \Rightarrow \widehat {BAD} = {180^0} - {120^0} = {60^0}$
Cách khác:
Xét tam giác \(ADE\), theo định lý về tổng ba góc trong tam giác, ta có:
\(\widehat {BAD} + \widehat {CDA} + \widehat {AED} = {180^0}\)
\(\begin{array}{l}
\Rightarrow \widehat {BAD} + \widehat {CDA} + {40^0} = {180^0}\\
\Rightarrow \widehat {BAD} + \widehat {CDA} = {140^0}\,(1*)
\end{array}\)
Xét tam giác \(ABF\), theo định lý về tổng ba góc trong tam giác, ta có:
\(\begin{array}{l}
\widehat {BAD} + \widehat {CBA} + \widehat {AFB} = {180^0}\\
\Rightarrow \widehat {BAD} + \widehat {CBA} + {20^0} = {180^0}\\
\Rightarrow \widehat {BAD} + \widehat {CBA} = {160^0}\,(2*)
\end{array}\)
Vì tứ giác \(ABCD\) nội tiếp đường tròn \((O)\) nên \(\widehat {ADC} + \widehat {CBA} = {180^0}\) (3*) (tổng hai góc đối bằng \(180^0\))
Từ \((1*), (2*)\) và (3*) ta có:
\(\begin{array}{l}
\widehat {BAD} + \widehat {ADC} + \widehat {BAD} + \widehat {CBA} = {140^0} + {160^0}\\
\Rightarrow 2\widehat {BAD} + \left( {\widehat {ADC} + \widehat {CBA}} \right) = {300^0}\\
\Rightarrow 2\widehat {BAD} + {180^0} = {300^0}\\
\Rightarrow 2\widehat {BAD} = {120^0}\\
\Rightarrow \widehat {BAD} = {60^0}
\end{array}\)
Cho \(\Delta ABC\) cân tại \(A\) có \(\widehat {BAC} = {120^0}.\) Trên nửa mặt phẳng bờ \(BC\) không chứa đỉnh \(A\), lấy \(D\) sao cho \(BCD\) là tam giác đều. Khi đó
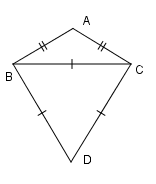
Ta có $\Delta BCD$ là tam giác đều nên \(\widehat {DCB} = {60^0}\,\,\left( 1 \right).\) Mặt khác \(\Delta ABC\) là tam giác cân tại \(A\) có $\widehat {BAC} = {120^0}$ hơn nữa tổng ba góc trong một tam giác bằng \({180^0}\) nên ta nhận được
\(\left\{ \begin{array}{l}\widehat {ACB} = \widehat {ABC}\\\widehat {ACB} + \widehat {ABC} + \widehat {BAC} = {180^0}\end{array} \right. \Rightarrow \widehat {ACB} = {30^0}\,\,\,\,\left( 2 \right)\) .
Từ \(\left( 1 \right)\) và \(\left( 2 \right)\) ta có \(\widehat {DCA} = \widehat {DCB} + \widehat {BCA} = {60^0} + {30^0} = {90^0}\,\,\left( 3 \right)\).
Chứng minh tương tự ta có \(\widehat {ABD} = {90^0}\,\,\left( 4 \right).\)
Từ \(\left( 3 \right)\) và \(\left( 4 \right)\) ta nhận được \(\widehat {ABD} + \widehat {DCA} = {90^0} + {90^0} = {180^0}\,.\)
Vậy tứ giác \(ABDC\) là tứ giác nội tiếp.
Cho tam giác $ABC$ nhọn nội tiếp đường tròn$\left( O \right)$ . $M$ là điểm thuộc cung nhỏ $AC$ (cung \(CM < \) cung \(AM\) ). Vẽ $MH$ vuông góc với $BC$ tại $H$ , vẽ $MI$ vuông góc với $AC$ tại $I$ . Chọn câu đúng:
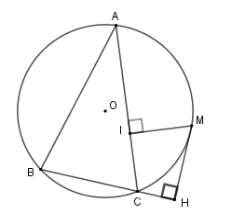
Xét tứ giác $IMHC$ ta có: $\widehat {MIC} = {90^0}$ ($MI$ vuông góc với$AC$ ); $\widehat {MHC} = {90^0}$($MH$ vuông góc với$BC$ )
$ \Rightarrow \widehat {{\rm{MIC}}} + \widehat {MHC} = {180^0}$ $ \Rightarrow $tứ giác $IMHC$ nội tiếp (dhnb).
Và tứ giác $IMHC$ chưa đủ điều kiện để là hình chữ nhật và hình vuông.
Cho đường tròn $(O)$ đường kính $AB.$ Gọi $H$ là điểm nằm giữa $O$ và $B.$ Kẻ dây $CD$ vuông góc với $AB$ tại $H$. Trên cung nhỏ $AC$ lấy điểm $E,$ kẻ $CK \bot AE$ tại $K.$ Đường thẳng $DE$ cắt $CK$ tại $F.$
Tứ giác \(AHCK\) là
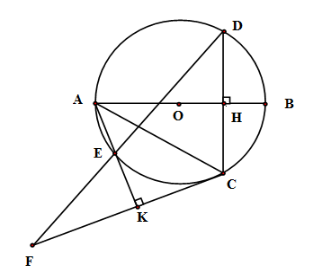
Tứ giác \(AHCK\) có \(\widehat {AHC} = 90^\circ \left( {AB \bot CD} \right);\widehat {AKC} = 90^\circ \left( {AK \bot FC} \right)\) nên \(\widehat {AHC} + \widehat {AKC} = 180^\circ \Rightarrow \) Tứ giác \(AHCK\) nội tiếp.
Cho đường tròn $(O)$ đường kính $AB.$ Gọi $H$ là điểm nằm giữa $O$ và $B.$ Kẻ dây $CD$ vuông góc với $AB$ tại $H$. Trên cung nhỏ $AC$ lấy điểm $E,$ kẻ $CK \bot AE$ tại $K.$ Đường thẳng $DE$ cắt $CK$ tại $F.$
Tích \(AH.AB\) bằng
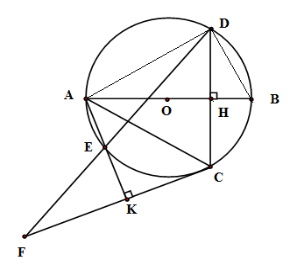
Xét tam giác \(ADB\) có \(\widehat {ADB} = 90^\circ \) (góc nội tiếp chắn nửa đường tròn) \( \Rightarrow \Delta ADB\) vuông tại \(D\)
Do đó \(A{D^2} = AH.AB\) (hệ thức lượng trong tam giác vuông)
Mà \(AD \ne BD;AD < AB\) nên phương án A, B, C sai.

