Câu hỏi:
2 năm trước
Cho đường tròn $\left( O \right)$ đường kính $AB$ . Gọi $H$ là điểm nằm giữa $O$ và $B$. Kẻ dây $CD$ vuông góc với $AB$ tại $H$ . Trên cung nhỏ $AC$ lấy điểm $E$ kẻ $CK$ vuông góc $AE$ tại $K$ . Đường thẳng $DE$ cắt $CK$ tại $F$. Chọn câu đúng:
Trả lời bởi giáo viên
Đáp án đúng: a
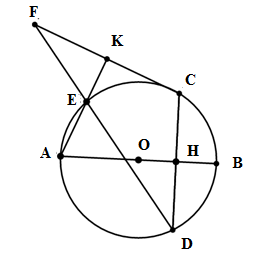
Có $\widehat {AHC} = {90^0}$(CD vuông góc AB); $\widehat {AKC} = {90^0}$ (AK vuông góc CF)
$ \Rightarrow \widehat {{\rm{AHC}}} + \widehat {AKC} = {180^0}$ $ \Rightarrow $ tứ giác AHCK nội tiếp \( \Rightarrow \) phương án A đúng, B sai.
\( \Rightarrow \widehat {EAO} + \widehat {HCK} = {180^0}\) (hai góc đối diện)\( \Rightarrow \) phương án C sai.
Xét tam giác vuông \(ADB\) có \(AH.AB = A{D^2}\) (hệ thức lượng trong tam giác vuông) nên phương án D sai.
Hướng dẫn giải:
Dấu hiệu nhận biết tứ giác nội tiếp:
+) Tứ giác có tổng hai góc đối diện bằng \({180^0}.\)
+) Tứ giác có hai đỉnh kề một cạnh cùng nhìn cạnh chứa hai đỉnh còn lại dưới một góc \(\alpha .\)
+) Tứ giác có bốn đỉnh cách đều một điểm, điểm đó là tâm của đường tròn ngoại tiếp tứ giác.
+) Tứ giác có góc ngoài tại một đỉnh bằng góc trong tại đỉnh đối của đỉnh đó.
