Tứ giác nội tiếp

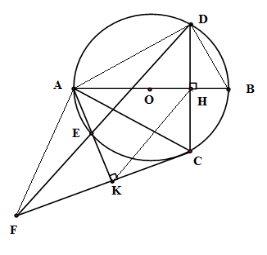
Xét $\left( O \right)$ có $\widehat {EAC} = \widehat {EDC}$ (hai góc nội tiếp cùng chắn một cung)

Xét tứ giác nội tiếp $AHCK$ có $\widehat {KAC} = \widehat {KHC}$  nên $\widehat {EDC} = \widehat {KHC}\left( { = \widehat {KAC}} \right)$ mà hai góc ở vị trí đồng vị nên $KH{\rm{//}}ED$

Xét tam giác $CFD$ có $KH{\rm{//}}ED$mà $H$ là trung điểm của $DC$ ( do $AB \bot DC$) nên $K$ là trung điểm của $CF$

Xét tam giác $ACF$ có $AK$ vừa là đường trung tuyến vừa là đường cao nên $\Delta ACF$ cân tại $A$ .

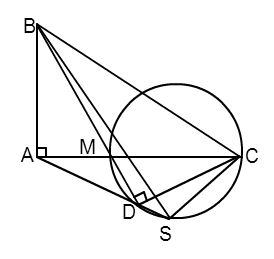
+) Ta có: $\widehat {MDC}$ là góc nội tiếp chắn nửa đường tròn đường kính $MC$ $\Rightarrow \widehat {MDC} = {90^0}$ (tính chất góc nội tiếp).

Xét tứ giác $ABCD$ ta có:

Góc $BAC$ và góc $BDC$ cùng nhìn đoạn $BC$ dưới góc ${90^0}.$

$\Rightarrow$ $ABCD$ là tứ giác nội tiếp (dhnb) $\Rightarrow$ phương án A đúng.

+) Xét tứ giác $ABCD$ nội tiếp ta có$\widehat {ABD} = \widehat {ACD}$ (cùng nhìn đoạn $AD$ )$\Rightarrow$ phương án B đúng.

+) Xét đường tròn đường kính $MC$ ta có $4$  điểm $M,C,D,S$ cùng thuộc đường tròn.

$\Rightarrow$ Tứ giác $MCSD$ là tứ giác nội tiếp.

$\Rightarrow \widehat {ADM} = \widehat {SCM}$ (góc ngoài tại $1$  đỉnh bằng góc trong tại đỉnh đối diện). $\left( 1 \right)$

Vì tứ giác $ABCD$ nội tiếp (cmt) $\Rightarrow \widehat {ACB} = \widehat {ADB}$ (cùng nhìn đoạn$AB$ )    $\left( 2 \right)$

Từ $\left( 1 \right)$ và $\left( 2 \right)$ $\Rightarrow \widehat {BCA} = \widehat {ACS}\;\;\;\left( { = \widehat {ADB}} \right).$

Hay $CA$ là phân giác của $\widehat {SCB} \Rightarrow$ phương án C đúng.

+) Giả sử tứ giác $ABCS$ là tứ giác nội tiếp $\Rightarrow \widehat {ASB} = \widehat {BCA}$ (hai góc cùng nhìn đoạn $AB$ ).

Mà $\widehat {ACB} = \widehat {BDA};\;\;\;\widehat {BAD} \ne \widehat {BSA}$ (xét trong đường tròn đường kính $CM$ )

$\Rightarrow \widehat {ASB} \ne \widehat {BCA} \Rightarrow$ tứ giác $ABCS$ không là tứ giác nội tiếp $\Rightarrow$phương án D sai.

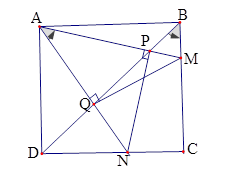
Xét hình vuông $ABCD$ có $\widehat {DBC} = \widehat {BDC} = 45^\circ$ (tính chất)

Xét tứ giác $ABMQ$ có $\widehat {QAM} = \widehat {QBM} = 45^\circ$ mà hai đỉnh $A$ và $B$ cùng nhìn đoạn thẳng $MQ$ nên $ABMQ$ là tứ giác nội tiếp.

Xét tứ giác $APND$ có $\widehat {PAN} = \widehat {PDN} = 45^\circ$ mà hai đỉnh $A$ và ${\rm{D}}$ cùng nhìn đoạn thẳng $PN$ nên $APND$ là tứ giác nội tiếp.

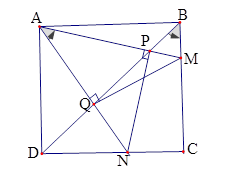
Từ kết quả câu trước ta suy ra $\widehat {ADP} = \widehat {ANP} = {45^0},\widehat {QAM} = \widehat {QBM} = {45^0}$$\Rightarrow NP \bot AM,MQ \bot AN$. Tập hợp các điểm $P,Q,C$ nhìn đoạn $MN$ dưới một góc vuông, nên các điểm này nằm trên đường tròn đường kính $MN$.

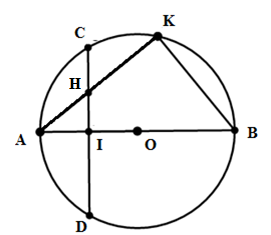
Ta có: $\widehat {AKB}$ là góc nội tiếp chắn nửa đường tròn (O) $\Rightarrow \widehat {AKB} = {90^0} \,\left( {t/c} \right).$

Xét tứ giác $HKBI$ ta có

$\left\{ \begin{array}{l}\;\widehat {HKB} = {90^0}\\\widehat {HIB} = {90^0}\left( {do\;\;CD \bot AB = \left\{ I \right\}} \right)\end{array} \right. \Rightarrow \widehat {HKB} + \widehat {HIB} = {180^0}$ .

$\Rightarrow$ Tứ giác $BKHI$ là tứ giác nội tiếp (dhnb) $\Rightarrow$phương án A đúng, phương  án B sai.

Lại có $\widehat {KBA} < {90^0}$ do $\Delta AKB$ vuông tại  $K \Rightarrow KBIH$ không là hình chữ nhật.

$\Rightarrow$ phương  án C sai.

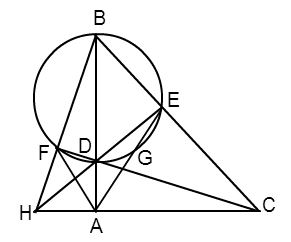
+) Xét đường tròn đường kính $BD$ có góc $BED$ là góc nội tiếp chắn nửa đường tròn $\Rightarrow \widehat {BED} = {90^0}.$

Xét $\Delta ABC$ và $\Delta BED$ ta có: $\widehat {DBE}\;\;chung$ và $\widehat {BAC} = \widehat {BED} = {90^0}$$\Rightarrow \Delta ABC\backsim\Delta EBD\;\left( {g - g} \right)$ $\Rightarrow$ phương án A đúng.

+) Xét tứ giác $ADEC$ có: $\widehat {DEC} + \widehat {DAC} = {90^0} + {90^0} = {180^0}$

$\Rightarrow$Tứ giác $ADEC$ là tứ giác nội tiếp (dhnb).$\Rightarrow$ Đáp án B đúng.

+) Chứng minh tương tự ta được tứ giác $AFBC$ là tứ giác nội tiếp $\Rightarrow$ phương án C sai.

+) Gọi giao điểm của $BF$ và $AC$ là$H$ .

  Xét tam giác $BHC$ có hai đường cao $CF$ và $BA$ cắt nhau tại$D$   $\Rightarrow$$D$  là trực tâm của tam giác $BHC$

Mà $DE$ $\bot$$AB$  $\Rightarrow$$DE$  là đường cao của tam giác $BHC$ hay $H,E,D$ thẳng hàng.         

$\Rightarrow$$DE,AC$  và $BF$ đồng quy tại$H$   $\Rightarrow$phương án D đúng.

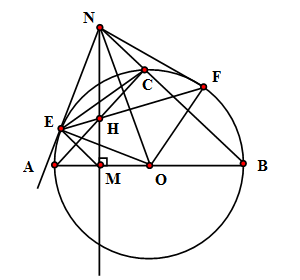
+) Vì $\widehat {NEO} = \widehat {NMO} = 90^\circ  \Rightarrow NEMO$ là tứ giác nội tiếp nên bốn điểm $O,E,M,N$ cùng thuộc một đường tròn

$\Rightarrow$ Phương án A đúng.

+) $\widehat {NEC} = \widehat {CBE} = \dfrac{1}{2}$ số đo cung $CE \Rightarrow \Delta NEC\backsim\Delta NBE\left( {g - g} \right) \Rightarrow \dfrac{{NE}}{{NB}} = \dfrac{{NC}}{{NE}}$ $\Rightarrow NB.NC = N{E^2}$

$\Rightarrow$ Phương án B đúng.

+) Hai tam giác vuông $\Delta NCH\backsim\Delta NMB\left( {g - g} \right)$

$\Rightarrow \dfrac{{NC}}{{NM}} = \dfrac{{NH}}{{NB}}$

$\Rightarrow NC.NB=NH.NM$

Từ đó $\Delta NEH\backsim\Delta NME\left( {c-g -c} \right) \Rightarrow \widehat {NEH} = \widehat {EMN}$ $\Rightarrow$ Phương án C đúng.

+) $\widehat {EMN} = \widehat {EON}$ (tứ giác $NEMO$ nội tiếp) $\Rightarrow \widehat {NEH} = \widehat {NOE}$ 

Mà góc $ENO$ phụ với góc $EON$ nên góc $ENO$ cũng phụ với góc $NEH$

$\Rightarrow EH \bot NO$ 

$\Rightarrow \Delta OEF$ cân có $ON$ là phân giác

$\Rightarrow \widehat {EON} = \widehat {NOF} \Rightarrow \widehat {NEF} = \widehat {NOF}$  nên tứ giác $NEOF$ nội tiếp $\Rightarrow \widehat {NFO} = 180^\circ  - \widehat {NEO} = 90^\circ$ .

$\Rightarrow$ Phương án D sai.

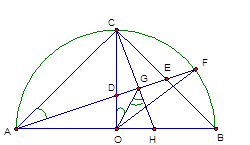
Theo giả thiết ta có $OC \bot AB,\,CG \bot AG$ nên ta suy ra $\widehat {AOC} = \widehat {AGC} = {90^0}.$

Nói cách khác $O,\,G$ cùng nhìn $AC$ dưới một góc vuông.
Do đó tứ giác ACGO nội tiếp đường tròn đường kính $AC$  nên  $\widehat {OGA} = \widehat {OCA}.$

Mà $\Delta OAC$ vuông cân tại O nên $\widehat {OCA} = {45^0}.$ Suy ra $\widehat {OGA} = {45^0}.$ Ta lại có $\widehat {OGH} + \widehat {OGA} = \widehat {HGA} = \widehat {AGC} = {90^0} \Rightarrow \widehat {OGH} = {90^0} - \widehat {OGA} = {90^0} - {45^0} = {45^0}.$

Do đó $\widehat {OGH} = {45^0}$

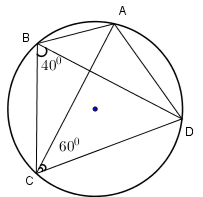
Do tứ giác $ABCD$ nội tiếp đường tròn tâm $O,$ nên ta có

$\widehat {CAD} = \widehat {CBD}$ (cùng chắn cung $CD$ ). Do đó ta có

$\widehat {CAD} = {40^0}.$

Tổng ba góc trong một tam giác bằng ${180^0}$

Nên:

$\begin{array}{l}\widehat {CAD} + \widehat {ACD} + \widehat {ADC} = {180^0}\\ \Rightarrow \widehat {ADC} = {180^0} - \left( {\widehat {CAD} + \widehat {ACD}} \right) \\= {180^0} - \left( {{{40}^0} + {{60}^0}} \right) = {80^0}.\end{array}$

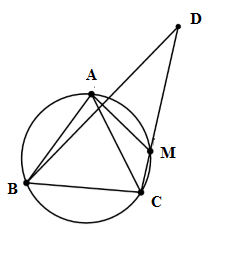
Xét tam giác ABC cân  tại A và $\widehat A = {60^0} \Rightarrow \widehat B = \widehat C = \dfrac{{{{180}^0} - \widehat A}}{2} = \dfrac{{{{180}^0} - \partial }}{2} = {90^0} - \dfrac{\partial }{2}.$

Ta có tứ giác AMCB là tứ giác nội tiếp (4 điểm A, M, B, C cùng thuộc (O)).

$\Rightarrow \widehat {AMC} = {180^0} - \widehat {ABC}$$= {180^0} - \left( {{{90}^0} - \dfrac{\partial }{2}} \right) = {90^0} + \dfrac{\partial }{2}.$ 

$\Rightarrow \widehat {DMA} = \widehat {ABC} = {90^0} - \dfrac{\partial }{2}$ (tính chất tứ giác nội tiếp).

Gọi I là giao điểm của AM và BD.

$\Rightarrow \Delta DMI$ vuông tại I.

$\Rightarrow \widehat {BDM} = {90^0} - \widehat {AMD}$$= {90^0} - \left( {{{90}^0} - \dfrac{\partial }{2}} \right) = \dfrac{\partial }{2}.$

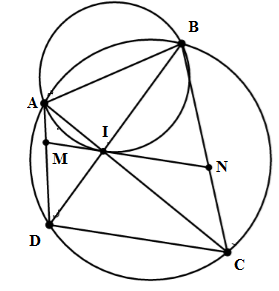
Xét đường tròn ngoại tiếp tam giác ABI ta có:

$\widehat {BAI}$ là góc nội tiếp chắn cung BI.

$\widehat {BIN}$ là góc tạo bởi tia tiếp tuyến và dây cung chắn cung BI.

$\Rightarrow \widehat {BAI} = \widehat {BIN}$ (góc nội tiếp và góc tạo bởi tia tiếp tuyến và dây cung cùng chắn cung BI).

Xét đường tròn (O) ta có:

$\widehat {BDC} = \widehat {BAC}$ (hai góc nội tiếp cùng chắn cung BC).

$\Rightarrow \widehat {BIN} = \widehat {BDC}\left( { = \widehat {BAC}} \right)$

Lại có hai góc này ở vị trí đồng vị

$\Rightarrow IN//CD\;\;hay\;\;MN//CD\;\;\left( {dpcm} \right).$

$\Rightarrow$ đáp án A đúng.

Do MN//CD nên $\widehat {MNC} + \widehat {NCD} = {180^0}$(trong cùng phía)

Mà do tứ giác ABCD nội tiếp nên $\widehat {MAB} + \widehat {NCD} = {180^0}$

=> $\widehat {MNC} = \widehat {NAB}$

=> Tứ giác ABNM nội tiếp (góc trong bằng góc ngoài tại đỉnh đối diện)

$\Rightarrow$ Đáp án B đúng.

+) Ta có: $IN//CD\;\;\left( {cmt} \right) \Rightarrow$ INCD là hình thang $\Rightarrow$ đáp án D đúng.

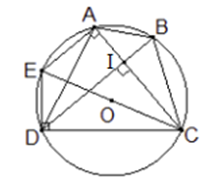
Vẽ  đường kính $CE$ của đường tròn $\left( O \right).$

Ta có $\widehat {EAC} = {90^0},\,\widehat {EDC} = {90^0}$ (góc nội tiếp chắn đường kính $EC$ ).

Từ đó ta có $AE \bot AC.$ Mặt khác theo giả thiết $AC \bot BD.$

Kéo theo $AE//BD.$ Vậy $AEDB$ là hình thang.

Do hình thang $AEDB$ nội tiếp $\left( O \right)$ nên nói phải là hình thang cân.

Kéo theo $AB = DE$ (các cạnh bên hình thang cân).

Từ đó ta có $A{B^2} + C{D^2} = D{E^2} + D{C^2} = E{C^2} = {\left( {2a} \right)^2} = 4{a^2}$ (do $\Delta EDC$ vuông tại $D).$

Áp dụng bất đẳng thức Cô-si cho $\left( {A{B^2},B{D^2}} \right)$ ta có $A{B^2} + B{D^2} \ge 2AB.CD$$\Rightarrow 2\left( {A{B^2} + B{D^2}} \right) \ge A{B^2} + B{D^2} + 2AB.CD$$= {\left( {AB + CD} \right)^2}.$

Kéo theo ${\left( {AB + CD} \right)^2} \le 2\left( {4{a^2}} \right) = 8{a^2}$$\Rightarrow AB + CD \le 2\sqrt 2 a.$

Đẳng thức xảy ra khi và chỉ khi $AB = CD.$

Xét tam giác $\Delta ABI,\,\,\Delta DCI$ có $AB = CD,$ $\widehat {ABD} = \widehat {ACD}$ (góc nội tiếp cùng chắn cung $AD),$ $\widehat {BAC} = \widehat {DCB}$ (góc nội tiếp cùng chắn cung $BC).$

Do đó $\Delta ABI = \Delta DCI\left( {g.c.g}. \right)$ Kéo theo $AI = ID,\,IB = IC.$ Suy ra $AC = AI + IC = ID + IB = BD.$

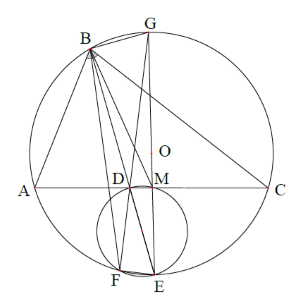
Gọi $M$ là trung điểm của $AC.$ Do $E$ là điểm chính giữa cung $AC$ nên $EM \bot AC.$

Do đó $EM$ đi qua tâm của đường tròn $\left( O \right).$ Giả sử rằng $G = DF \cap \left( O \right).$ Do $\widehat {DFE} = {90^0},$ nên

$\widehat {GFE} = {90^0},$ hay $GE$ là đường kính của $\left( O \right).$ Suy ra $G,M,E$ thẳng hàng.

Vì vậy $\widehat {GBE} = {90^0},$ mà $\widehat {GMD} = {90^0}.$

Kéo theo tứ giác $BDMG$ là tứ giác nội tiếp đường tròn đường kính $GD.$

Vì vậy $\widehat {MBD} = \widehat {DGM} = \widehat {FGE}\,\,\left( 1 \right)$ (cùng chắn cung $DM)$

 Lại có tứ giác $BFEG$ là tứ giác nội tiếp nên $\widehat {FBE} = \widehat {FGE}\,\,\left( 2 \right)\,$ ( cùng chắn cung $FE$ ).

Từ $\left( 1 \right)$ và $\left( 2 \right)$ ta suy ra $\widehat {MBD} = \widehat {FBE}.$ Do đó $BF$ và $BM$ đối xứng nhau qua $BD.$

Vì vậy $M \equiv N$ hay $N$ là trung điểm của $AC$ nên $AN = NC.$

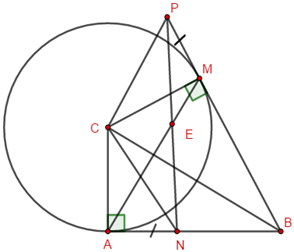
Ta có: tam giác $ABC$ vuông tại $A$ nên $\angle BAC = {90^0}$

$MB$ là tiếp tuyến của đường tròn $\left( {C;CA} \right)$ nên $\angle CMB = {90^0}$ (định nghĩa tiếp tuyến của đường tròn)

Xét tứ giác $ACMB$ ta có: $\angle CAB + \angle CMB = {90^0} + {90^0} = {180^0}$

$\Rightarrow ACMB$ là tứ giác nội tiếp đường tròn đường kính BC (tứ giác có tổng hai góc đối diện bằng ${180^0}$).

Hay bốn điểm $A,C,M$ và $B$ cùng thuộc đường tròn đường kính $BC$.

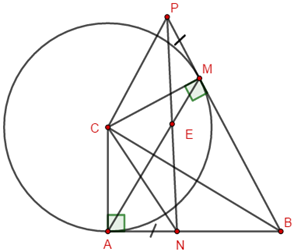
Xét tam giác $CAN$ và tam giác $CMP$ có:

$AN = MP\,\,\,\,\left( {gt} \right)$

$\angle CAN = \angle CMP = {90^0}$

$AC = CM$($A,M$ cùng thuộc đường tròn $\left( {C;\,\,CA} \right)$)

$\Rightarrow \Delta CAN = \Delta CMP\,\,\,\left( {c - g - c} \right)$

$\Rightarrow CN = CP$(2 cạnh tương ứng bằng nhau).

$\Rightarrow \Delta CNP$ cân tại $C$.

Gọi $E$ là giao điểm của $AM$ và $PN$.

Vì $\Delta CAN = \Delta CMP\,\,\,\left( {cmt} \right)$ nên:

$\angle ACN = \angle MCP$(2 góc tương ứng bằng nhau)

$\Rightarrow \angle ACM = \angle ACN + \angle NCM$ $= \angle PCM + \angle MCN = \angle NCP$

$\Rightarrow$$\Delta ACM$ và $\Delta CNP$ là hai tam giác cân đỉnh $C$ có $\angle ACM = \angle PCN$

$\Rightarrow \angle CNP = \angle CAM$ (các góc ở đáy của các tam giác cân có góc ở đỉnh bằng nhau)

Hay $\angle CAE = \angle CNE$

$\Rightarrow CANE$ là tứ giác nội tiếp. (tứ giác có hai đỉnh kề 1 cạnh cùng nhìn cạnh đối diện dưới các góc bằng nhau).

$\Rightarrow \angle CEN = {90^0} \Rightarrow CE \bot PN$

Mà $\Delta CNP$ cân tại $C$ (cmt)

$\Rightarrow CE$ là đường cao, đồng thời là đường trung tuyến của $\Delta CNP$

$\Rightarrow E$ là trung điểm của $PN$

Vậy đường thẳng $AM$ đi qua trung điểm của đoạn thẳng $NP$.