Câu hỏi:
3 năm trước
Cho tam giác \(ABC\) vuông tại \(A\). Vẽ đường tròn tâm \(C\), bán kính \(CA\). Từ điểm \(B\) kẻ tiếp tuyến \(BM\) với đường tròn \(\left( {C;CA} \right)\) (\(M\) là tiếp điểm, \(M\) và \(A\) nằm khác phía nhau đối với đường thẳng \(BC\)).
Chọn khẳng định đúng:
Trả lời bởi giáo viên
Đáp án đúng: c
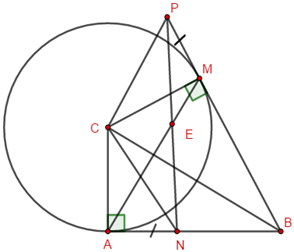
Ta có: tam giác \(ABC\) vuông tại \(A\) nên \(\angle BAC = {90^0}\)
\(MB\) là tiếp tuyến của đường tròn \(\left( {C;CA} \right)\) nên \(\angle CMB = {90^0}\) (định nghĩa tiếp tuyến của đường tròn)
Xét tứ giác \(ACMB\) ta có: \(\angle CAB + \angle CMB = {90^0} + {90^0} = {180^0}\)
\( \Rightarrow ACMB\) là tứ giác nội tiếp đường tròn đường kính BC (tứ giác có tổng hai góc đối diện bằng \({180^0}\)).
Hay bốn điểm \(A,C,M\) và \(B\) cùng thuộc đường tròn đường kính \(BC\).

