Tính: \(A = {\sin ^2}B + {\sin ^2}C - \tan B.\tan C\).
Xét tam giác vuông \(ABC\) có
Ta có: \(\sin B = \dfrac{{AC}}{{BC}} \Rightarrow {\sin ^2}B = \dfrac{{A{C^2}}}{{B{C^2}}}\)
\(\sin C = \dfrac{{AB}}{{BC}} \Rightarrow {\sin ^2}C = \dfrac{{A{B^2}}}{{B{C^2}}}\;\;\)
\(\tan B = \dfrac{{AC}}{{AB}} \Rightarrow \tan C = \dfrac{{AB}}{{AC}}\)
Vậy \(A = {\sin ^2}B + {\sin ^2}C - \tan B.\tan C\;\)
\( = \dfrac{{A{C^2}}}{{B{C^2}}} + \dfrac{{A{B^2}}}{{B{C^2}}} - \dfrac{{AC}}{{AB}}.\dfrac{{AB}}{{AC}} = \dfrac{{A{C^2} + A{B^2}}}{{B{C^2}}} - 1\) mà theo Pytago ta có \(A{B^2} + A{C^2} = B{C^2}\) nên
\(A = \dfrac{{B{C^2}}}{{B{C^2}}} - 1 = 0\)
Chọn câu đúng.
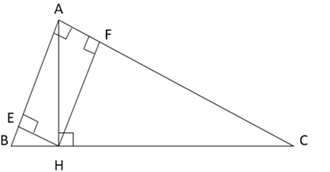
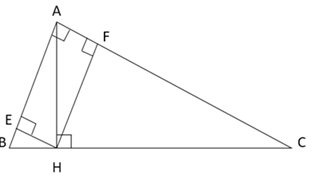
Xét tam giác vuông $AHB$ có đường cao $HE$ , ta có:
\(A{H^2} = AE.AB\)
Tương tự với tam giác vuông $AHC,$ ta có:
\(A{H^2} = AF.AC\)
Do đó: $AE.AB = AF.AC$
Tính \(EF.\)
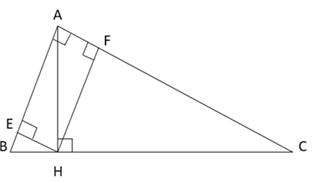
Ta có tam giác $ABC$ vuông tại $A$
\(AC = \sqrt {B{C^2} - A{B^2}} = \sqrt {{{10}^2} - {6^2}} = 8\)(cm)
Lại có: $AH$ là đường cao của tam giác vuông $ABC$ nên
\(AH.BC = AB.AC\) (hệ thức lượng trong tam giác vuông)
\( = > AH = \dfrac{{AB.AC}}{{BC}} = \dfrac{{6.8}}{{10}} = 4,8\left( {cm} \right)\)
Dễ thấy tứ giác $AFHE$ là hình chữ nhật (có 3 góc vuông)
Nên $EF = AH = 4,8\left( {cm} \right)$
Tính \(EF.\)

Ta có tam giác $ABC$ vuông tại $A$
\(AC = \sqrt {B{C^2} - A{B^2}} = \sqrt {{{10}^2} - {6^2}} = 8\)(cm)
Lại có: $AH$ là đường cao của tam giác vuông $ABC$ nên
\(AH.BC = AB.AC\) (hệ thức lượng trong tam giác vuông)
\( = > AH = \dfrac{{AB.AC}}{{BC}} = \dfrac{{6.8}}{{10}} = 4,8\left( {cm} \right)\)
Dễ thấy tứ giác $AFHE$ là hình chữ nhật (có 3 góc vuông)
Nên $EF = AH = 4,8\left( {cm} \right)$
Chọn câu đúng.
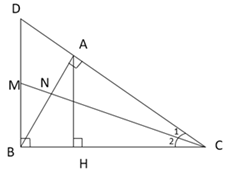
Ta có \(\Delta C{\rm A}{\rm N}\) đồng dạng với $\Delta CBM$ (g-g) (theo câu trước) nên \(\dfrac{{NA}}{{CA}} = \dfrac{{MB}}{{CB}}\;\left( 3 \right)\)
Tia $CM$ là phân giác của góc $BCD$ nên
\(\dfrac{{MB}}{{MD}} = \dfrac{{CB}}{{CD}} \Rightarrow \dfrac{{MB}}{{CB}} = \dfrac{{MD}}{{CD}}\) (4)
Từ (3) và (4) \( \Rightarrow \dfrac{{NA}}{{CA}} = \dfrac{{MD}}{{CD}} \Rightarrow \dfrac{{NA}}{{MD}} = \dfrac{{CA}}{{CD}}\).
Chọn câu đúng.
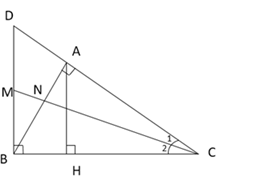
Ta có: \(\widehat {{C_1}} = \widehat {{C_2}}\) (gt)
\( \Rightarrow \Delta C{\rm A}{\rm N}\) đồng dạng với $\Delta CBM$ (g-g)
Suy ra \(\dfrac{{CN}}{{CM}} = \dfrac{{CA}}{{CB}}\,\,\left( 1 \right)\)
Lại có \(\Delta CAB\) đồng dạng với \(\Delta CBD\) (g-g)
Suy ra \(\dfrac{{CA}}{{CB}} = \dfrac{{CB}}{{CD}}\;\left( 2 \right)\)
Từ (1) và (2) \( \Rightarrow \dfrac{{CN}}{{CM}} = \dfrac{{CB}}{{CD}} \Rightarrow CN.CD = CM.CB\)
Chọn câu đúng.

Ta có: \(\widehat {{C_1}} = \widehat {{C_2}}\) (gt)
\( \Rightarrow \Delta C{\rm A}{\rm N}\) đồng dạng với $\Delta CBM$ (g-g)
Suy ra \(\dfrac{{CN}}{{CM}} = \dfrac{{CA}}{{CB}}\,\,\left( 1 \right)\)
Lại có \(\Delta CAB\) đồng dạng với \(\Delta CBD\) (g-g)
Suy ra \(\dfrac{{CA}}{{CB}} = \dfrac{{CB}}{{CD}}\;\left( 2 \right)\)
Từ (1) và (2) \( \Rightarrow \dfrac{{CN}}{{CM}} = \dfrac{{CB}}{{CD}} \Rightarrow CN.CD = CM.CB\)
Kẻ \(BK \bot AC\). Tính tỷ số $\dfrac{{AK}}{{AC}}$.
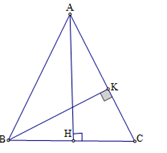
Ta có \(\dfrac{1}{2}BC.AH = \dfrac{1}{2}BK.AC = {S_{ABC}}\)
Suy ra \(BK = \dfrac{{BC.AH}}{{AC}} = \dfrac{{2a}}{b}\sqrt {{b^2} - {a^2}} \).
Áp dụng định lý Pitago trong tam giác vuông \(AKB\) ta có: \(A{K^2} = A{B^2} - B{K^2} = {b^2} - \dfrac{{4{a^2}}}{{{b^2}}}\left( {{b^2} - {a^2}} \right) = \dfrac{{{{\left( {{b^2} - 2{a^2}} \right)}^2}}}{{{b^2}}}\).
Suy ra \(AK = \dfrac{{\left| {{b^2} - 2{a^2}} \right|}}{b}\) do đó $\dfrac{{AK}}{{AC}} = \dfrac{{\left| {{b^2} - 2{a^2}} \right|}}{{{b^2}}}$.
Tính diện tích tam giác $ABC$
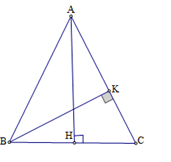
Gọi \(H\) là trung điểm của \(BC\). Theo định lý Pitago ta có:
\(A{H^2} = A{C^2} - H{C^2} = {b^2} - {a^2}\)\( \Rightarrow AH = \sqrt {{b^2} - {a^2}} \)
Suy ra \({S_{ABC}} = \dfrac{1}{2}BC.AH = \dfrac{1}{2}.2a\sqrt {{b^2} - {a^2}}= a\sqrt {{b^2} - {a^2}}\)
Tính diện tích tam giác $ABC$

Gọi \(H\) là trung điểm của \(BC\). Theo định lý Pitago ta có:
\(A{H^2} = A{C^2} - H{C^2} = {b^2} - {a^2}\)\( \Rightarrow AH = \sqrt {{b^2} - {a^2}} \)
Suy ra \({S_{ABC}} = \dfrac{1}{2}BC.AH = \dfrac{1}{2}.2a\sqrt {{b^2} - {a^2}}= a\sqrt {{b^2} - {a^2}}\)
Tính \(EF.\)

Ta có tam giác $ABC$ vuông tại $A$
\(AC = \sqrt {B{C^2} - A{B^2}} = \sqrt {{{10}^2} - {6^2}} = 8\)(cm)
Lại có: $AH$ là đường cao của tam giác vuông $ABC$ nên
\(AH.BC = AB.AC\) (hệ thức lượng trong tam giác vuông)
\( = > AH = \dfrac{{AB.AC}}{{BC}} = \dfrac{{6.8}}{{10}} = 4,8\left( {cm} \right)\)
Dễ thấy tứ giác $AFHE$ là hình chữ nhật (có 3 góc vuông)
Nên $EF = AH = 4,8\left( {cm} \right)$
Chọn câu đúng.

Ta có: \(\widehat {{C_1}} = \widehat {{C_2}}\) (gt)
\( \Rightarrow \Delta C{\rm A}{\rm N}\) đồng dạng với $\Delta CBM$ (g-g)
Suy ra \(\dfrac{{CN}}{{CM}} = \dfrac{{CA}}{{CB}}\,\,\left( 1 \right)\)
Lại có \(\Delta CAB\) đồng dạng với \(\Delta CBD\) (g-g)
Suy ra \(\dfrac{{CA}}{{CB}} = \dfrac{{CB}}{{CD}}\;\left( 2 \right)\)
Từ (1) và (2) \( \Rightarrow \dfrac{{CN}}{{CM}} = \dfrac{{CB}}{{CD}} \Rightarrow CN.CD = CM.CB\)
Tính diện tích tam giác $ABC$

Gọi \(H\) là trung điểm của \(BC\). Theo định lý Pitago ta có:
\(A{H^2} = A{C^2} - H{C^2} = {b^2} - {a^2}\)\( \Rightarrow AH = \sqrt {{b^2} - {a^2}} \)
Suy ra \({S_{ABC}} = \dfrac{1}{2}BC.AH = \dfrac{1}{2}.2a\sqrt {{b^2} - {a^2}}= a\sqrt {{b^2} - {a^2}}\)
Cho tam giác $ABC$ vuông tại $A$ có $AB = 6cm,{\rm{ }}BC = 10cm,$ đường cao $AH.$ Gọi $E,{\rm{ }}F$ là hình chiếu của $H$ lần lượt lên $AB,{\rm{ }}AC.$
Tính \(EF.\)

Ta có tam giác $ABC$ vuông tại $A$
\(AC = \sqrt {B{C^2} - A{B^2}} = \sqrt {{{10}^2} - {6^2}} = 8\)(cm)
Lại có: $AH$ là đường cao của tam giác vuông $ABC$ nên
\(AH.BC = AB.AC\) (hệ thức lượng trong tam giác vuông)
\( = > AH = \dfrac{{AB.AC}}{{BC}} = \dfrac{{6.8}}{{10}} = 4,8\left( {cm} \right)\)
Dễ thấy tứ giác $AFHE$ là hình chữ nhật (có 3 góc vuông)
Nên $EF = AH = 4,8\left( {cm} \right)$
Cho tam giác $ABC$ vuông tại $A$ có $AB = 6cm,{\rm{ }}BC = 10cm,$ đường cao $AH.$ Gọi $E,{\rm{ }}F$ là hình chiếu của $H$ lần lượt lên $AB,{\rm{ }}AC.$
Chọn câu đúng.

Xét tam giác vuông $AHB$ có đường cao $HE$ , ta có:
\(A{H^2} = AE.AB\)
Tương tự với tam giác vuông $AHC,$ ta có:
\(A{H^2} = AF.AC\)
Do đó: $AE.AB = AF.AC$
Cho tam giác $ABC$ vuông tại $A$ có $AB = 6cm,{\rm{ }}BC = 10cm,$ đường cao $AH.$ Gọi $E,{\rm{ }}F$ là hình chiếu của $H$ lần lượt lên $AB,{\rm{ }}AC.$
Tính: \(A = {\sin ^2}B + {\sin ^2}C - \tan B.\tan C\).

Xét tam giác vuông \(ABC\) có
Ta có: \(\sin B = \dfrac{{AC}}{{BC}} \Rightarrow {\sin ^2}B = \dfrac{{A{C^2}}}{{B{C^2}}}\)
\(\sin C = \dfrac{{AB}}{{BC}} \Rightarrow {\sin ^2}C = \dfrac{{A{B^2}}}{{B{C^2}}}\;\;\)
\(\tan B = \dfrac{{AC}}{{AB}} \Rightarrow \tan C = \dfrac{{AB}}{{AC}}\)
Vậy \(A = {\sin ^2}B + {\sin ^2}C - \tan B.\tan C\;\)
\( = \dfrac{{A{C^2}}}{{B{C^2}}} + \dfrac{{A{B^2}}}{{B{C^2}}} - \dfrac{{AC}}{{AB}}.\dfrac{{AB}}{{AC}} = \dfrac{{A{C^2} + A{B^2}}}{{B{C^2}}} - 1\) mà theo Pytago ta có \(A{B^2} + A{C^2} = B{C^2}\) nên
\(A = \dfrac{{B{C^2}}}{{B{C^2}}} - 1 = 0\)
Cho tam giác $ABC$ vuông tại $A$ có đường cao $AH.$ Qua $B$ vẽ đường thẳng vuông góc với $BC$ cắt đường thẳng $AC$ tại $D.$ Tia phân giác của góc $C$ cắt $AB$ tại $N$ và $BD$ tại $M.$
Chọn câu đúng.

Ta có: \(\widehat {{C_1}} = \widehat {{C_2}}\) (gt)
\( \Rightarrow \Delta C{\rm A}{\rm N}\) đồng dạng với $\Delta CBM$ (g-g)
Suy ra \(\dfrac{{CN}}{{CM}} = \dfrac{{CA}}{{CB}}\,\,\left( 1 \right)\)
Lại có \(\Delta CAB\) đồng dạng với \(\Delta CBD\) (g-g)
Suy ra \(\dfrac{{CA}}{{CB}} = \dfrac{{CB}}{{CD}}\;\left( 2 \right)\)
Từ (1) và (2) \( \Rightarrow \dfrac{{CN}}{{CM}} = \dfrac{{CB}}{{CD}} \Rightarrow CN.CD = CM.CB\)
Cho tam giác $ABC$ vuông tại $A$ có đường cao $AH.$ Qua $B$ vẽ đường thẳng vuông góc với $BC$ cắt đường thẳng $AC$ tại $D.$ Tia phân giác của góc $C$ cắt $AB$ tại $N$ và $BD$ tại $M.$
Chọn câu đúng.

Ta có \(\Delta C{\rm A}{\rm N}\) đồng dạng với $\Delta CBM$ (g-g) (theo câu trước) nên \(\dfrac{{NA}}{{CA}} = \dfrac{{MB}}{{CB}}\;\left( 3 \right)\)
Tia $CM$ là phân giác của góc $BCD$ nên
\(\dfrac{{MB}}{{MD}} = \dfrac{{CB}}{{CD}} \Rightarrow \dfrac{{MB}}{{CB}} = \dfrac{{MD}}{{CD}}\) (4)
Từ (3) và (4) \( \Rightarrow \dfrac{{NA}}{{CA}} = \dfrac{{MD}}{{CD}} \Rightarrow \dfrac{{NA}}{{MD}} = \dfrac{{CA}}{{CD}}\).
Cho tam giác cân \(ABC\) có đáy \(BC = 2a\), cạnh bên bằng \(b\left( {b > a} \right)\).
Tính diện tích tam giác $ABC$

Gọi \(H\) là trung điểm của \(BC\). Theo định lý Pitago ta có:
\(A{H^2} = A{C^2} - H{C^2} = {b^2} - {a^2}\)\( \Rightarrow AH = \sqrt {{b^2} - {a^2}} \)
Suy ra \({S_{ABC}} = \dfrac{1}{2}BC.AH = \dfrac{1}{2}.2a\sqrt {{b^2} - {a^2}}= a\sqrt {{b^2} - {a^2}}\)
Cho tam giác cân \(ABC\) có đáy \(BC = 2a\), cạnh bên bằng \(b\left( {b > a} \right)\).
Kẻ \(BK \bot AC\). Tính tỷ số $\dfrac{{AK}}{{AC}}$.

Ta có \(\dfrac{1}{2}BC.AH = \dfrac{1}{2}BK.AC = {S_{ABC}}\)
Suy ra \(BK = \dfrac{{BC.AH}}{{AC}} = \dfrac{{2a}}{b}\sqrt {{b^2} - {a^2}} \).
Áp dụng định lý Pitago trong tam giác vuông \(AKB\) ta có: \(A{K^2} = A{B^2} - B{K^2} = {b^2} - \dfrac{{4{a^2}}}{{{b^2}}}\left( {{b^2} - {a^2}} \right) = \dfrac{{{{\left( {{b^2} - 2{a^2}} \right)}^2}}}{{{b^2}}}\).
Suy ra \(AK = \dfrac{{\left| {{b^2} - 2{a^2}} \right|}}{b}\) do đó $\dfrac{{AK}}{{AC}} = \dfrac{{\left| {{b^2} - 2{a^2}} \right|}}{{{b^2}}}$.

