Câu hỏi:
2 năm trước
Cho tam giác $ABC$ vuông tại $A$ có đường cao $AH.$ Qua $B$ vẽ đường thẳng vuông góc với $BC$ cắt đường thẳng $AC$ tại $D.$ Tia phân giác của góc $C$ cắt $AB$ tại $N$ và $BD$ tại $M.$
Chọn câu đúng.
Trả lời bởi giáo viên
Đáp án đúng: c
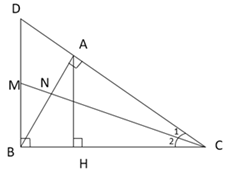
Ta có \(\Delta C{\rm A}{\rm N}\) đồng dạng với $\Delta CBM$ (g-g) (theo câu trước) nên \(\dfrac{{NA}}{{CA}} = \dfrac{{MB}}{{CB}}\;\left( 3 \right)\)
Tia $CM$ là phân giác của góc $BCD$ nên
\(\dfrac{{MB}}{{MD}} = \dfrac{{CB}}{{CD}} \Rightarrow \dfrac{{MB}}{{CB}} = \dfrac{{MD}}{{CD}}\) (4)
Từ (3) và (4) \( \Rightarrow \dfrac{{NA}}{{CA}} = \dfrac{{MD}}{{CD}} \Rightarrow \dfrac{{NA}}{{MD}} = \dfrac{{CA}}{{CD}}\).
Hướng dẫn giải:
Sử dụng tính chất hai tam giác đồng dạng và tính chất đường phân giác để tìm hệ thức đúng.
Câu hỏi khác
- Bài tập một số hệ thức về cạnh và đường cao trong tam giác vuông toán 9 có lời giải
- Bài tập một số hệ thức về cạnh và góc trong tam giác vuông toán 9 có lời giải
- Bài tập tỉ số lượng giác của góc nhọn toán 9 có lời giải
- Bài tập ứng dụng thực tế tỉ số lượng giác của góc nhọn toán 9 có lời giải
- Bài tập hay và khó chương hệ thức lượng trong tam giác vuông toán 9 có lời giải
