Cho tam giác $ABC$ vuông tại $A$ có $AB = 6cm,{\rm{ }}BC = 10cm,$ đường cao $AH.$ Gọi $E,{\rm{ }}F$ là hình chiếu của $H$ lần lượt lên $AB,{\rm{ }}AC.$

Tính: \(A = {\sin ^2}B + {\sin ^2}C - \tan B.\tan C\).

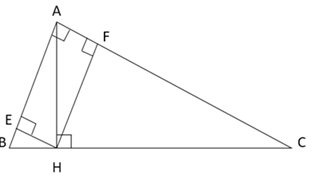
Xét tam giác vuông \(ABC\)  có

Ta có: \(\sin B = \dfrac{{AC}}{{BC}} \Rightarrow {\sin ^2}B = \dfrac{{A{C^2}}}{{B{C^2}}}\)

\(\sin C = \dfrac{{AB}}{{BC}} \Rightarrow {\sin ^2}C = \dfrac{{A{B^2}}}{{B{C^2}}}\;\;\)

\(\tan B = \dfrac{{AC}}{{AB}} \Rightarrow \tan C = \dfrac{{AB}}{{AC}}\)

Vậy \(A = {\sin ^2}B + {\sin ^2}C - \tan B.\tan C\;\)

\( = \dfrac{{A{C^2}}}{{B{C^2}}} + \dfrac{{A{B^2}}}{{B{C^2}}} - \dfrac{{AC}}{{AB}}.\dfrac{{AB}}{{AC}} = \dfrac{{A{C^2} + A{B^2}}}{{B{C^2}}} - 1\)  mà theo Pytago ta có \(A{B^2} + A{C^2} = B{C^2}\)  nên

\(A = \dfrac{{B{C^2}}}{{B{C^2}}} - 1 = 0\)