Câu hỏi:
2 năm trước
Cho tam giác cân \(ABC\) có đáy \(BC = 2a\), cạnh bên bằng \(b\left( {b > a} \right)\).
Kẻ \(BK \bot AC\). Tính tỷ số $\dfrac{{AK}}{{AC}}$.
Trả lời bởi giáo viên
Đáp án đúng: c
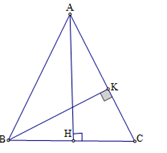
Ta có \(\dfrac{1}{2}BC.AH = \dfrac{1}{2}BK.AC = {S_{ABC}}\)
Suy ra \(BK = \dfrac{{BC.AH}}{{AC}} = \dfrac{{2a}}{b}\sqrt {{b^2} - {a^2}} \).
Áp dụng định lý Pitago trong tam giác vuông \(AKB\) ta có: \(A{K^2} = A{B^2} - B{K^2} = {b^2} - \dfrac{{4{a^2}}}{{{b^2}}}\left( {{b^2} - {a^2}} \right) = \dfrac{{{{\left( {{b^2} - 2{a^2}} \right)}^2}}}{{{b^2}}}\).
Suy ra \(AK = \dfrac{{\left| {{b^2} - 2{a^2}} \right|}}{b}\) do đó $\dfrac{{AK}}{{AC}} = \dfrac{{\left| {{b^2} - 2{a^2}} \right|}}{{{b^2}}}$.
Hướng dẫn giải:
Sử dụng diện tích tam giác \(ABC\) đã tính ở câu trước và định lý Pytago để tính \(AK\) , từ đó suy ra tỉ số \(\dfrac{{AK}}{{AC}}.\)
Câu hỏi khác
- Bài tập một số hệ thức về cạnh và đường cao trong tam giác vuông toán 9 có lời giải
- Bài tập một số hệ thức về cạnh và góc trong tam giác vuông toán 9 có lời giải
- Bài tập tỉ số lượng giác của góc nhọn toán 9 có lời giải
- Bài tập ứng dụng thực tế tỉ số lượng giác của góc nhọn toán 9 có lời giải
- Bài tập hay và khó chương hệ thức lượng trong tam giác vuông toán 9 có lời giải
