Chọn khẳng định đúng?
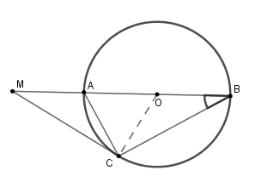
Tam giác $OBC$ cân tại $O$ có \(\widehat {ABC} = 30^\circ \) suy ra $\widehat {AOC} = 60^\circ $ (góc ngoài tại một đỉnh bằng tổng hai góc trong không kề với nó).
Nên tam giác $OCA$ là tam giác đều suy ra \(AC = AO = AM = R.\) \( \Rightarrow \widehat {OCM} = {90^ \circ } \Rightarrow MC\) là tiếp tuyến của \((O;R).\)
Tứ giác $AMON$ là hình gì?
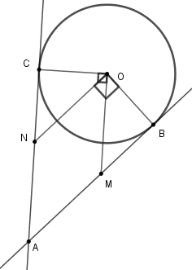
Dễ có $AMON$ là hình bình hành (Vì $ON{\rm{//}}AM;OM{\rm{//}}AN$).
Ta chứng minh \(OM = ON\).
Xét tam giác $OBM$ và tam giác $OCN$ có :
\(\widehat {OBM} = \widehat {OCN} = {90^0};\)
\({\rm{ }}OB = OC = R,\)
và \(\widehat {OMB} = \widehat {ONC} = \widehat A \)
\(\Rightarrow \Delta OBM = \Delta OCN\)
\( \Rightarrow OM = ON \Rightarrow AMON\) là hình thoi .
Chọn khẳng định đúng?
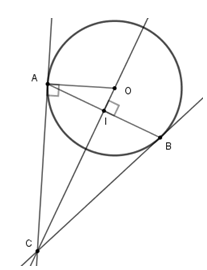
Ta có: \(OC \bot AB\) \( \Rightarrow \) $OC$ đi qua trung điểm của $AB$.
\( \Rightarrow \)$OC$ là đường cao đồng thời là trung tuyến của\(\Delta ABC\).
\( \Rightarrow \)\(\Delta ABC\) cân tại $C$.
\( \Rightarrow \)\(\left\{ \begin{array}{l}\widehat {ACO} = \widehat {BCO}\\AC = CB\end{array} \right.\)\( \Rightarrow \Delta AOC = \Delta BOC\left( {c - g - c} \right)\)
\( \Rightarrow OB \bot BC\)
\( \Rightarrow \)$BC$ là tiếp tuyến của $\left( O \right)$
Xác định tâm $F$ của đường tròn đi qua bốn điểm $A,D,H,E$.
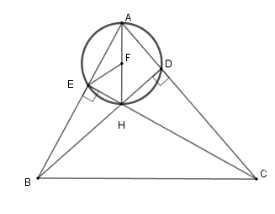
Gọi $F$ là trung điểm của $AH$
Xét hai tam giác vuông $AEH$ và $ADH$ ta có $FA = FH = FE = FD = \dfrac{{AH}}{2}$
Nên bốn đỉnh $A,D,H,E$ cùng thuộc đường tròn tâm $F$ bán kính $\dfrac{{AH}}{2}$.
Độ dài bán kính $OB$ là
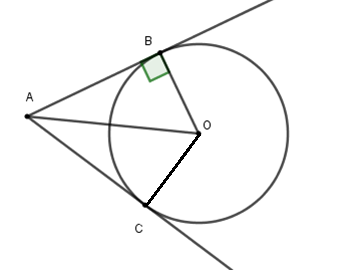
Từ hình vẽ ta có $AB;AC$ là tiếp tuyến của $\left( O \right)$ tại $B,C$ suy ra $OC \bot AC$ tại $C$.
Suy ra $\Delta ABO = \Delta ACO\left( {c - g - c} \right)$ nên $\widehat {BAO} = \widehat {CAO} = \dfrac{{\widehat {BAC}}}{2} = 30^\circ $
Xét $\Delta ABO$ có $OB = AO.\sin A = 10.\sin 30^\circ = 5\,cm$
Tính độ dài $MC$ theo $R.$
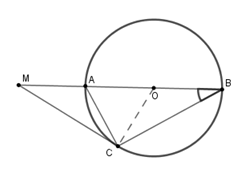
Áp dụng định lý Pytago cho tam giác vuông $OCM$, ta có \(O{M^2} = O{C^2} + M{C^2}\)\( \Rightarrow M{C^2} = O{M^2} - O{C^2} = 3{R^2} \Rightarrow MC = \sqrt 3 R.\)
Chọn khẳng định đúng?

Tam giác $OBC$ cân tại $O$ có \(\widehat {ABC} = 30^\circ \) suy ra $\widehat {AOC} = 60^\circ $ (góc ngoài tại một đỉnh bằng tổng hai góc trong không kề với nó).
Nên tam giác $OCA$ là tam giác đều suy ra \(AC = AO = AM = R.\) \( \Rightarrow \widehat {OCM} = {90^ \circ } \Rightarrow MC\) là tiếp tuyến của \((O;R).\)
Chọn khẳng định đúng?

Tam giác $OBC$ cân tại $O$ có \(\widehat {ABC} = 30^\circ \) suy ra $\widehat {AOC} = 60^\circ $ (góc ngoài tại một đỉnh bằng tổng hai góc trong không kề với nó).
Nên tam giác $OCA$ là tam giác đều suy ra \(AC = AO = AM = R.\) \( \Rightarrow \widehat {OCM} = {90^ \circ } \Rightarrow MC\) là tiếp tuyến của \((O;R).\)
Điểm $A$ phải cách $O$ một khoảng là bao nhiêu để cho $MN$ là tiếp tuyến của $\left( O \right)$?
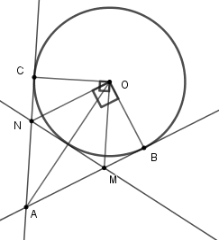
Tứ giác $AMON$ là hình thoi nên \(OA \bot MN\) và
Mà độ dài $OA$ bằng $2$ lần khoảng cách từ $O$ đến$MN$ .
Do đó $MN$ là tiếp tuyến đường tròn \(\left( {O;{\rm{ R}}} \right) \Leftrightarrow \) khoảng cách từ $O$ đến $MN$ bằng R \( \Leftrightarrow OA = 2R\).
Tứ giác $AMON$ là hình gì?

Dễ có $AMON$ là hình bình hành (Vì $ON{\rm{//}}AM;OM{\rm{//}}AN$).
Ta chứng minh \(OM = ON\).
Xét tam giác $OBM$ và tam giác $OCN$ có :
\(\widehat {OBM} = \widehat {OCN} = {90^0};\)
\({\rm{ }}OB = OC = R,\)
và \(\widehat {OMB} = \widehat {ONC} = \widehat A \)
\(\Rightarrow \Delta OBM = \Delta OCN\)
\( \Rightarrow OM = ON \Rightarrow AMON\) là hình thoi .
Tứ giác $AMON$ là hình gì?

Dễ có $AMON$ là hình bình hành (Vì $ON{\rm{//}}AM;OM{\rm{//}}AN$).
Ta chứng minh \(OM = ON\).
Xét tam giác $OBM$ và tam giác $OCN$ có :
\(\widehat {OBM} = \widehat {OCN} = {90^0};\)
\({\rm{ }}OB = OC = R,\)
và \(\widehat {OMB} = \widehat {ONC} = \widehat A \)
\(\Rightarrow \Delta OBM = \Delta OCN\)
\( \Rightarrow OM = ON \Rightarrow AMON\) là hình thoi .
Cho bán kính của đường tròn bằng $15\,cm$; $AB = 24cm$. Tính $OC$
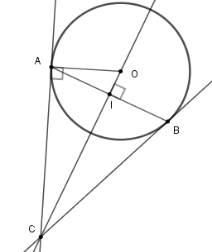
Gọi $I$ là giao điểm của $OC$ và$AB \Rightarrow AI = BI = \dfrac{{AB}}{2} = 12\,cm$
Xét tam giác vuông $OAI$ có $OI = \sqrt {O{A^2} - A{I^2}} = 9\,cm$
Xét tam giác vuông $AOC$ có $A{O^2} = OI.OC \Rightarrow OC = \dfrac{{A{O^2}}}{{OI}} = \dfrac{{{{15}^2}}}{9} = 25\,cm$
Vậy $OC = 25\,cm$.
Chọn khẳng định đúng?

Ta có: \(OC \bot AB\) \( \Rightarrow \) $OC$ đi qua trung điểm của $AB$.
\( \Rightarrow \)$OC$ là đường cao đồng thời là trung tuyến của\(\Delta ABC\).
\( \Rightarrow \)\(\Delta ABC\) cân tại $C$.
\( \Rightarrow \)\(\left\{ \begin{array}{l}\widehat {ACO} = \widehat {BCO}\\AC = CB\end{array} \right.\)\( \Rightarrow \Delta AOC = \Delta BOC\left( {c - g - c} \right)\)
\( \Rightarrow OB \bot BC\)
\( \Rightarrow \)$BC$ là tiếp tuyến của $\left( O \right)$
Chọn khẳng định đúng?

Ta có: \(OC \bot AB\) \( \Rightarrow \) $OC$ đi qua trung điểm của $AB$.
\( \Rightarrow \)$OC$ là đường cao đồng thời là trung tuyến của\(\Delta ABC\).
\( \Rightarrow \)\(\Delta ABC\) cân tại $C$.
\( \Rightarrow \)\(\left\{ \begin{array}{l}\widehat {ACO} = \widehat {BCO}\\AC = CB\end{array} \right.\)\( \Rightarrow \Delta AOC = \Delta BOC\left( {c - g - c} \right)\)
\( \Rightarrow OB \bot BC\)
\( \Rightarrow \)$BC$ là tiếp tuyến của $\left( O \right)$
“Nếu một đường thẳng đi qua một điểm của đường tròn và … thì đường thẳng ấy là một tiếp tuyến của đường tròn”. Cụm từ thích hợp điền vào chỗ trống là
Nếu một đường thẳng đi qua một điểm của đường tròn và vuông góc với bán kính đi qua điểm đó thì đường thẳng ấy là một tiếp tuyến của đường tròn.
Cho \(\left( {O;4cm} \right)\). Đường thẳng \(d\) là tiếp tuyến của đường tròn \(\left( {O;4\,cm} \right)\), khi đó
Khoảng cách từ tâm của một đường tròn đến tiếp tuyến bằng bán kính của đường tròn đó.
Cho tam giác \(MNP\) có \(MN = 5cm,NP = 12cm,MP = 13cm\). Vẽ đường tròn \(\left( {M;NM} \right)\). Khẳng định nào sau đây là đúng?
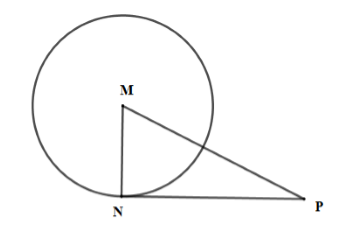
+) Xét tam giác \(MNP\) có \(M{P^2} = {13^2} = 169;N{M^2} + N{P^2} = {5^2} + {12^2} = 169\)\( \Rightarrow M{P^2} = N{M^2} + N{P^2}\)
\( \Rightarrow \Delta MNP\) vuông tại N (định lý Pytago đảo)
\( \Rightarrow MN \bot NP\) mà \(N \in \left( {M;MN} \right)\) nên \(NP\) là tiếp tuyến của \(\left( {M;MN} \right)\)
Độ dài đoạn \(AB\) là
Vì \(AB;AC\) là tiếp tuyến của \(\left( O \right)\) tại \(B,C\) suy ra \(OB \bot AB\) tại \(B\) và \(OC \bot AC\) tại \(C.\)
Từ đó \(\Delta ABO = \Delta ACO\left( {c - g - c} \right)\) nên \(\widehat {BAO} = \widehat {CAO} = \dfrac{{\widehat {BAC}}}{2} = 60^\circ \)
Xét \(\Delta ABO\) có \(AB = AO.\cos A = 8.\cos 60^\circ = 4\).
Độ dài bán kính \(OB\) là
Vì \(AB;AC\) là tiếp tuyến của \(\left( O \right)\) tại \(B,C\) suy ra \(OB \bot AB\) tại \(B\) và \(OC \bot AC\) tại \(C.\)
Từ đó \(\Delta ABO = \Delta ACO\left( {c - g - c} \right)\) nên \(\widehat {BAO} = \widehat {CAO} = \dfrac{{\widehat {BAC}}}{2} = 60^\circ \)
Xét \(\Delta ABO\) có \(OB = AO.\sin A = 8.\sin 60^\circ = 4\sqrt 3 \,cm\)
Độ dài bán kính \(OB\) là
Vì \(AB;AC\) là tiếp tuyến của \(\left( O \right)\) tại \(B,C\) suy ra \(OB \bot AB\) tại \(B\) và \(OC \bot AC\) tại \(C.\)
Từ đó \(\Delta ABO = \Delta ACO\left( {c - g - c} \right)\) nên \(\widehat {BAO} = \widehat {CAO} = \dfrac{{\widehat {BAC}}}{2} = 60^\circ \)
Xét \(\Delta ABO\) có \(OB = AO.\sin A = 8.\sin 60^\circ = 4\sqrt 3 \,cm\)

