Cho hàm số \(y = a{x^2}\,\,\) với \(a \ne 0\). Kết luận nào sau đây là đúng?
Cho hàm số \(y = {\rm{a}}{{\rm{x}}^2}\,\,(a \ne 0)\).
a) Nếu \(a > 0\) thì hàm số nghịch biến \(x < 0\) khi và đồng biến khi \(x > 0\).
b) Nếu \(a < 0\) thì hàm số đồng biến khi \(x < 0\) và nghịch biến khi \(x > 0\).
Giá trị của hàm số \(y = f\left( x \right) = \dfrac{4}{5}{x^2}\) tại \({x_0} = - 5\) là
Thay \({x_0} = - 5\) vào hàm số \(y = f\left( x \right) = \dfrac{4}{5}{x^2}\) ta được \(f\left( { - 5} \right) = \dfrac{4}{5}.{\left( { - 5} \right)^2} = 20\)
Cho hàm số \(y = f\left( x \right) = \dfrac{{2m - 3}}{3}{x^2}\) . Tìm giá trị của \(m\) để đồ thị đi qua điểm \(B\left( { - 3;5} \right)\)
Thay tọa độ điểm \(B\left( { - 3;5} \right)\) vào hàm số \(y = f\left( x \right) = \dfrac{{2m - 3}}{3}{x^2}\) ta được
\(\dfrac{{2m - 3}}{3}.{\left( { - 3} \right)^2} = 5 \Leftrightarrow 3\left( {2m - 3} \right) = 5 \Leftrightarrow 6m - 9 = 5 \Leftrightarrow 6m = 14 \Leftrightarrow m = \dfrac{7}{3}\)
Vậy \(m = \dfrac{7}{3}\) là giá trị cần tìm.
Cho hàm số \(y = f\left( x \right) = \dfrac{1}{2}{x^2}\) . Tổng các giá trị của \(a\) thỏa mãn \(f\left( a \right) = 3 + \sqrt 5 \) là
Ta có \(f\left( a \right) = 3 + \sqrt 5 \)\( \Leftrightarrow \dfrac{1}{2}{a^2} = 3 + \sqrt 5 \)\( \Leftrightarrow {a^2} = 6 + 2\sqrt 5 \)\( \Leftrightarrow {a^2} =5+2\sqrt 5.1+1\)\(\Leftrightarrow {a^2} =(\sqrt 5)^2+2\sqrt 5.1+1^2\)\( \Leftrightarrow {a^2} = {\left( {\sqrt 5 + 1} \right)^2}\)
\( \Leftrightarrow \left[ \begin{array}{l}a = \sqrt 5 + 1\\a = - \sqrt 5 - 1\end{array} \right.\)
Vậy tổng các giá trị của \(a\) là \(\left( {\sqrt 5 + 1} \right) + \left( { - \sqrt 5 - 1} \right) = 0\)
Cho hàm số \(y = f\left( x \right) = - 2{x^2}\). Tìm \(b\) biết \(f\left( b \right) \le - 5b + 2\).
Ta có \(f\left( b \right) \le - 5b + 2\) \( \Leftrightarrow - 2{b^2} \le - 5b + 2 \Leftrightarrow 2{b^2} - 5b + 2 \ge 0\)\( \Leftrightarrow 2{b^2} - 4b - b + 2 \ge 0 \Leftrightarrow 2b\left( {b - 2} \right) - \left( {b - 2} \right) \ge 0 \Leftrightarrow \left( {2b - 1} \right)\left( {b - 2} \right) \ge 0\)
\( \Leftrightarrow \left[ \begin{array}{l}\left\{ \begin{array}{l}2b - 1 \ge 0\\b - 2 \ge 0\end{array} \right.\\\left\{ \begin{array}{l}2b - 1 \le 0\\b - 2 \le 0\end{array} \right.\end{array} \right. \Leftrightarrow \left[ \begin{array}{l}\left\{ \begin{array}{l}b \ge \dfrac{1}{2}\\b \ge 2\end{array} \right.\\\left\{ \begin{array}{l}b \le \dfrac{1}{2}\\b \le 2\end{array} \right.\end{array} \right. \Leftrightarrow \left[ \begin{array}{l}b \ge 2\\b \le \dfrac{1}{2}\end{array} \right.\)
Vậy \(\left[ \begin{array}{l}b \le \dfrac{1}{2}\\b \ge 2\end{array} \right.\) là giá trị cần tìm.
Cho hàm số \(y = \left( { - 3m + 1} \right){x^2}\). Tìm \(m\) để đồ thị hàm số đi qua điểm \(A\left( {x;y} \right)\) với \(\left( {x;y} \right)\) là nghiệm của hệ phương trình \(\left\{ \begin{array}{l}4x - 3y = - 2\\x - 2y = - 3\end{array} \right.\)
Ta có \(\left\{ \begin{array}{l}4x - 3y = - 2\\x - 2y = - 3\end{array} \right.\)\( \Leftrightarrow \left\{ \begin{array}{l}x = 2y - 3\\4\left( {2y - 3} \right) - 3y = - 2\end{array} \right. \Leftrightarrow \left\{ \begin{array}{l}x = 2y - 3\\5y = 10\end{array} \right. \Leftrightarrow \left\{ \begin{array}{l}y = 2\\x = 1\end{array} \right.\)\( \Rightarrow A\left( {1;2} \right)\)
Thay \(x = 1;y = 2\) vào hàm số \(y = \left( { - 3m + 1} \right){x^2}\) ta được
\(2 = \left( { - 3m + 1} \right){.1^2} \Leftrightarrow - 3m + 1 = 2 \Leftrightarrow - 3m = 1 \Leftrightarrow m = \dfrac{{ - 1}}{3}\)
Vậy \(m = - \dfrac{1}{3}\) là giá trị cần tìm.
Cho hàm số \(y = \dfrac{{m - 7}}{{ - 3}}{x^2}\) với \(m \ne 7\). Tìm \(m\) để hàm số nghịch biến với mọi \(x < 0\)
Để hàm số nghịch biến với mọi \(x < 0\) thì \(a > 0\) nên \(\dfrac{{m - 7}}{{ - 3}} > 0\)
\(\Leftrightarrow m - 7 < 0\) (do \(-3<0)\)
\(\Leftrightarrow m < 7\).
Vậy \(m < 7\) thỏa mãn điều kiện đề bài
Cho hàm số \(y = \dfrac{2}{{5 - 2m}}{x^2}\) với \(m \ne \dfrac{5}{2}\). Tìm \(m\) để hàm số đồng biến với mọi \(x < 0\)
Để hàm số đồng biến với mọi \(x < 0\) thì \(a < 0\) nên \(\dfrac{2}{{5 - 2m}} < 0\)
\( \Leftrightarrow 5 - 2m < 0 \) (do \(2>0)\)
\(\Leftrightarrow 2m > 5 \Leftrightarrow m > \dfrac{5}{2}\).
Vậy \(m > \dfrac{5}{2}\) thỏa mãn điều kiện đề bài
Cho hàm số \(y = \left( {4{m^2} + 12m + 11} \right){x^2}\) . Kết luận nào sau đây là sai?
Ta thấy hàm số \(y = \left( {4{m^2} + 12m + 11} \right){x^2}\) có
\(a = 4{m^2} + 12m + 11 = \left( {4{m^2} + 12m + 9} \right) + 2 \\= {\left( {2m + 3} \right)^2} + 2 \ge 2 > 0,\,\,\forall m\)
Nên hàm số đồng biến khi \(x > 0\) và nghịch biến khi \(x < 0\). Suy ra C sai, D đúng.
Và đồ thị hàm số nằm phía trên trục hoành, O là điểm thấp nhất của đồ thị.
Hình vẽ dưới đây là của đồ thị hàm số nào?
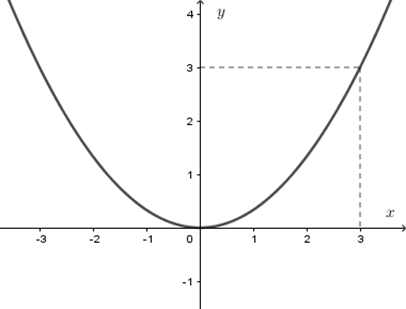
Từ hình vẽ ta thấy đồ thị đi qua điểm có tọa độ \(\left( {3;3} \right)\), ta thay \(x = 3;y = 3\) vào từng hàm số ở các đáp án ta được:
+ Đáp án A: \(y = {x^2} \Leftrightarrow 3 = {3^2} \Leftrightarrow 3 = 9\) (vô lý) nên loại A.
+ Đáp án B: \(y = \dfrac{1}{2}{x^2} \Leftrightarrow 3 = \dfrac{1}{2}{3^2} \Leftrightarrow 3 = \dfrac{9}{2}\) (vô lý) nên loại B.
+ Đáp án C: \(y = 3{x^2} \Leftrightarrow 3 = {3.3^2} \Leftrightarrow 3 = 27\) (vô lý) nên loại C.
+ Đáp án D: \(y = \dfrac{1}{3}{x^2} \Leftrightarrow 3 = \dfrac{1}{3}{.3^2} \Leftrightarrow 3 = 3\) (luôn đúng) nên chọn D.
Cho hàm số \(y = - \dfrac{2}{5}{x^2}\,\,\)có đồ thị là \((P)\). Điểm trên \(\left( P \right)\) (khác gốc tọa độ \(O\left( {0;0} \right)\)) có tung độ gấp ba lần hoành độ thì có hoành độ là:
Gọi điểm \(M\)\(\left( {x;y} \right)\) là điểm cần tìm. Vì \(M\) có tung độ gấp ba lần hoành độ nên \(M\left( {x;3x} \right)\).
Thay tọa độ điểm \(M\) vào hàm số ta được
\(3x = - \dfrac{2}{5}{x^2} \Leftrightarrow \dfrac{2}{5}{x^2} + 3x = 0 \\\Leftrightarrow x\left( {\dfrac{2}{5}x + 3} \right) = 0\left[ \begin{array}{l}x = 0 \Rightarrow y = 0\\x = - \dfrac{{15}}{2} \Rightarrow y = \dfrac{{ - 45}}{2}\end{array} \right.\)
Hay điểm khác gốc tọa độ thỏa mãn điều kiện là \(M\left( {\dfrac{{ - 15}}{2};\dfrac{{ - 45}}{2}} \right)\).
Trong các điểm \(A(5;5);B( - 5; - 5);C(10;20);D\left( {\sqrt {10} ;2} \right)\) có bao nhiêu điểm không thuộc đồ thị hàm số \(y = \dfrac{1}{5}{x^2}\,\left( P \right)\)
+) Thay tọa độ điểm \(A\left( {5;5} \right)\) vào hàm số \(y = \dfrac{1}{5}{x^2}\) ta được \(5 = \dfrac{1}{5}{.5^2} \Leftrightarrow 5 = 5\) (luôn đúng) nên \(A \in \left( P \right)\)
+) Thay tọa độ điểm \(B\left( { - 5; - 5} \right)\) vào hàm số \(y = \dfrac{1}{5}{x^2}\) ta được \( - 5 = \dfrac{1}{5}{\left( { - 5} \right)^2} \Leftrightarrow - 5 = 5\) ( vô lý) nên \(B \notin \left( P \right)\)
+) Thay tọa độ điểm \(D\left( {\sqrt {10} ;2} \right)\) vào hàm số \(y = \dfrac{1}{5}{x^2}\) ta được \(2 = \dfrac{1}{5}.{\left( {\sqrt {10} } \right)^2} \Leftrightarrow 2 = 2\) ( luôn đúng) nên \(D \in \left( P \right)\)
+) Thay tọa độ điểm \(C\left( {10;20} \right)\) vào hàm số \(y = \dfrac{1}{5}{x^2}\) ta được \(20 = \dfrac{1}{5}{.10^2} \Leftrightarrow 20 = 20\) (luôn đúng) nên \(B \in \left( P \right)\).
Vậy có 1 điểm không thuộc \(\left( P \right):y = \dfrac{1}{5}{x^2}\) là điểm \(B\left( { - 5; - 5} \right)\)
Cho \((P):y = 3{x^2};(d):y = - 4x - 1\). Tìm toạ độ giao điểm của \((P)\) và \((d)\).
Xét phương trình hoành độ giao điểm của parabol \(\left( P \right)\) và đường thẳng \((d):\) \(3{x^2} = - 4x - 1 \)\(\Leftrightarrow 3{x^2} + 4x + 1 = 0 \\\Leftrightarrow 3{x^2} + 3x + x + 1 = 0 \\\Leftrightarrow 3x\left( {x + 1} \right) + x + 1 = 0\)\( \Leftrightarrow \left( {3x + 1} \right)\left( {x + 1} \right) = 0 \\\Leftrightarrow \left[ \begin{array}{l}3x + 1 = 0\\x + 1 = 0\end{array} \right.\\ \Leftrightarrow \left[ \begin{array}{l}x = - \dfrac{1}{3} \Rightarrow y = 3{x^2} = \dfrac{1}{3}\\x = - 1 \Rightarrow y = 3{x^2} = 3\end{array} \right.\)
Nên tọa độ giao điểm cần tìm là \(\left( { - \dfrac{1}{3};\dfrac{1}{3}} \right);\left( { - 1;3} \right)\).
Cho parabol \(y = - \sqrt 5 {x^2}\). Xác định m để điểm \(A\left( {m\sqrt 5 ; - 2\sqrt 5 } \right)\) nằm trên parabol.
Thay \(x = m\sqrt 5 ;y = - 2\sqrt 5 \) vào hàm số \(y = - \sqrt 5 {x^2}\) ta được \( - 2\sqrt 5 = - \sqrt 5 .{\left( {m\sqrt 5 } \right)^2} \\\Leftrightarrow 5m^2\sqrt 5 = 2\sqrt 5 \Leftrightarrow m ^2= \dfrac{2}{5}\)
Vậy \(m =\pm \dfrac{\sqrt 10}{5}.\)
Cho parabol\((P):y = \sqrt {5m + 1} .{x^2}\) và đường thẳng \((d):y = 5x + 4\). Tìm \(m\) để đường thẳng \(d\) cắt \(\left( P \right)\) tại điểm có tung độ \(y = 9\).
ĐK: \(m > \dfrac{{ - 1}}{5}\)
Thay \(y = 9\) vào phương trình đường thẳng \(d\) ta được \(9 = 5x + 4 \Leftrightarrow x = 1\)
Nên tọa độ giao điểm của đường thẳng \(d\) và parabol \(\left( P \right)\) là \(\left( {1;9} \right)\)
Thay \(x = 1;y = 9\) vào hàm số \(y = \sqrt {5m + 1} .{x^2}\) ta được
\(\sqrt {5m + 1} {.1^2} = 9 \Leftrightarrow \sqrt {5m + 1} = 9 \Leftrightarrow 5m + 1 = 81 \Leftrightarrow 5m = 80 \Leftrightarrow m = 16\left( {TM} \right)\)
Vậy \(m = 16\) là giá trị cần tìm.
Cho parabol\((P):y = \left( {\sqrt {3m + 4} - \dfrac{7}{4}} \right){x^2}\) và đường thẳng \((d):y = 3x - 5\). Biết đường thẳng \(d\) cắt \(\left( P \right)\) tại một điểm có tung độ \(y = 1\). Tìm \(m\) và hoành độ giao điểm còn lại của \(d\) và parabol \(\left( P \right)\).
Thay \(y = 1\) vào phương trình đường thẳng \(d\) ta được \(3x - 5 = 1 \Leftrightarrow x = 2\)
Nên tọa độ giao điểm của đường thẳng \(d\) và parabol \(\left( P \right)\) là \(\left( {2;1} \right)\)
Thay \(x = 2;y = 1\) vào hàm số \(y = \left( {\sqrt {3m + 4} - \dfrac{7}{4}} \right){x^2}\) ta được
\(\left( {\sqrt {3m + 4} - \dfrac{7}{4}} \right){.2^2} = 1 \Leftrightarrow \sqrt {3m + 4} - \dfrac{7}{4} = \dfrac{1}{4} \Leftrightarrow \sqrt {3m + 4} = 2 \Leftrightarrow 3m + 4 = 4 \Leftrightarrow m = 0\)\( \Rightarrow \left( P \right):y = \dfrac{1}{4}{x^2}\)
Xét phương trình hoành độ giao điểm của \(d\) và \(\left( P \right)\) :
\(\dfrac{1}{4}{x^2} = 3x - 5 \Leftrightarrow {x^2} - 12x + 20 = 0 \Leftrightarrow \left( {x - 2} \right)\left( {x - 10} \right) = 0 \Leftrightarrow \left[ \begin{array}{l}x = 2\\x = 10\end{array} \right.\)
Vậy hoành độ giao điểm còn lại là \(x = 10.\)
Cho đồ thị hàm số \(y = \dfrac{1}{2}{x^2}\) \(\left( P \right)\) như hình vẽ. Dựa vào đồ thị, tìm \(m\) để phương trình \({x^2} - 2m + 4 = 0\) có hai nghiệm phân biệt.
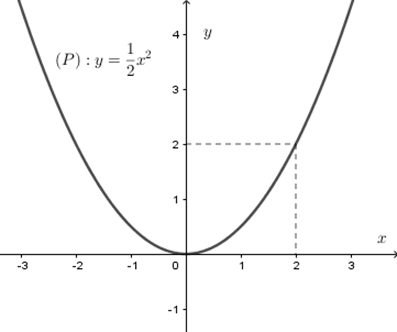
Xét phương trình \({x^2} - 2m + 4 = 0\) (*) \( \Leftrightarrow {x^2} = 2m - 4 \Leftrightarrow \dfrac{1}{2}{x^2} = m - 2\)
Số nghiệm của phương trình (*) là số giao điểm của parabol \(\left( P \right):y = \dfrac{1}{2}{x^2}\) và đường thẳng \(d:y = m - 2\).
Để (*) có hai nghiệm phân biệt thì \(d\) cắt \(\left( P \right)\) tại hai điểm phân biệt.
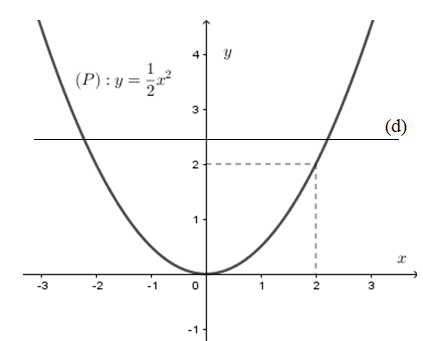
Từ đồ thị hàm số ta thấy:
Với \(m - 2 > 0 \Leftrightarrow m > 2\) thì \(d\) cắt \(\left( P \right)\) tại hai điểm phân biệt hay phương trình (*) có hai nghiệm phân biệt khi \(m > 2\).
Xác định hàm số \(y = a{x^2}\) biết rằng đồ thị của hàm số đi qua điểm \(A\left( { - 2;5} \right)\).
Vì đồ thị của hàm số \(y = a{x^2}\) đi qua điểm \(A\left( { - 2;5} \right)\) nên ta có: \(5 = a.{\left( { - 2} \right)^2} \Leftrightarrow a = \dfrac{5}{4}\).
Vậy \(y = \dfrac{5}{4}{x^2}\).
Giá trị của hàm số \(y = 2{x^2}\) tại \(x = 3\) là
Thay \(x = 3\) vào hàm số \(y = 2{x^2}\) ta có: \(y = {2.3^2} = 18\).
Vậy giá trị của hàm số \(y = 2{x^2}\) tại \(x = 3\) là \(18\).
Cho hàm số \(y = 3{x^2}.\) Kết luận nào sau đây đúng?
Hàm số \(y = 3{x^2}\) có \(a = 3 > 0\) nên hàm số nghịch biến khi \(x < 0\), đồng biến khi \(x > 0\).

