Cho hàm số: \(y = \left( {5m + 10} \right).{x^2}\) . Tìm \(m\) để hàm số đồng biến khi \(x > 0\).
Để hàm số \(y = \left( {5m + 10} \right).{x^2}\) đồng biến khi \(x > 0\) \( \Leftrightarrow a > 0 \Leftrightarrow 5m + 10 > 0 \Leftrightarrow m > - 2\)
Vậy \(m > - 2\) thỏa mãn bài toán.
Cho parabol \(y = f\left( x \right) = a{x^2}\). Cho biết \(\left( P \right)\) đi qua điểm \(A(\sqrt 3 ; - 3)\). Xác định giá trị của \(n\) để \(f\left( {{n^2}} \right) = f\left( {2n} \right)\)
\(\left( P \right)\) đi qua điểm \(A(\sqrt 3 ; - 3)\) nên toạ độ của nó phải thoả mãn phương trình \(y = a{x^2}\).
Ta có \( - 3 = a{(\sqrt 3 )^2} \Rightarrow a = - 1 \Rightarrow y = f\left( x \right) = - {x^2}\).
\(\begin{array}{l}f\left( {{n^2}} \right) = f\left( {2n} \right) \Leftrightarrow - {\left( {{n^2}} \right)^2} = - {\left( {2n} \right)^2} \Leftrightarrow {n^4} = 4{n^2}\\ \Leftrightarrow {n^2}({n^2} - 4) = 0 \Leftrightarrow \left[ \begin{array}{l}n = 0\\n = 2\\n = - 2\end{array} \right..\end{array}\)
Một quả bóng bàn được thả rơi tự do. Quãng đường chyển động \(s\) của nó được biểu diễn gần đúng bởi công thức \(s = 3{t^2},\) với \(t\) là thời gian tính bằng giây, \(s\) tính bằng mét. Quả bóng bàn đó được thả tự do từ độ cao \(108m.\) Thời gian quả bóng bàn đó tiếp đất là:
Khi quả bóng bàn tiếp đất thì ta có \(s = 108m.\)
\( \Rightarrow 3{t^2} = 108 \Leftrightarrow {t^2} = 36 \Leftrightarrow t = 6\,\left( s \right)\,\,\,\,\,\,\left( {do\,\,\,t > 0} \right).\)
Tìm \(m\) để hàm số \(y = \left( {2m - 3} \right){x^2}\) đồng biến khi \(x < 0.\)
Hàm số đã cho đồng biến khi \(x < 0\)
\( \Leftrightarrow 2m - 3 < 0 \Leftrightarrow m < \dfrac{3}{2}.\)
Cho parabol \(y = f\left( x \right) = a{x^2}\). tìm khẳng định đúng
Ta có:
\(\begin{array}{l}f\left( 3 \right) + f\left( 4 \right) = a{.3^2} + a{.4^2} = a\left( {{3^2} + {4^2}} \right) = a.25 = a{.5^2} = f\left( 5 \right)\\f\left( 4 \right) + f\left( 5 \right) = a{.4^2} + a{.5^2} = a\left( {{4^2} + {5^2}} \right) = a.41 \ne a{.6^2} = f\left( 6 \right)\\f\left( 6 \right) + f\left( 7 \right) = a{.6^2} + a{.7^2} = a\left( {{6^2} + {7^2}} \right) = a.85 \ne a{.8^2} = f\left( 8 \right)\end{array}\)
Cho hàm số \(y = \left( {1 - \sqrt {m - 1} } \right){x^2}.\) Hàm số đã cho đồng biến khi \(x < 0\) nếu:
Hàm số đồng biến khi \(x < 0\) thì \(1 - \sqrt {m - 1} < 0 \Rightarrow m > 2\)
Cho hàm số \(y = - 3{x^2}.\) Khẳng định nào dưới đây đúng?
Ta có: \(a = - 3 < 0 \Rightarrow \) hàm số đồng biến khi \(x < 0\) và nghịch biến khi \(x > 0.\)
Cho parabol\((P):y = 5{x^2}\) và đường thẳng \((d):y = - 4x - 4\). Số giao điểm của đường thẳng \(d\) và parabol \(\left( P \right)\) là:
Xét phương trình hoành độ giao điểm của parabol \(\left( P \right)\) và đường thẳng \((d):\)
\(5{x^2} = - 4x - 4 \Leftrightarrow 5{x^2} + 4x + 4 = 0 \\\Leftrightarrow {x^2} + 4{x^2} + 4x + 4 = 0 \\\Leftrightarrow {x^2} + {\left( {x + 2} \right)^2} = 0\,\,\left( * \right)\)
Xét \({x^2} + {\left( {x + 2} \right)^2} \ge 0;\forall x\) và dấu “=” xảy ra khi \(\left\{ \begin{array}{l}x = 0\\x + 2 = 0\end{array} \right. \Leftrightarrow \left\{ \begin{array}{l}x = 0\\x = - 2\end{array} \right.\) (vô lý) nên \({x^2} + {\left( {x + 2} \right)^2} > 0;\forall x\)
Hay phương trình (*) vô nghiệm.
Vậy không có giao điểm của đường thẳng \((d)\) và parabol \(\left( P \right)\).
Biết đồ thị hàm số \(y = a{x^2}\) đi qua điểm \(A\left( { - 1; - 2} \right),\) giá trị của \(a\) bằng:
Ta có đồ thị hàm số \(y = a{x^2}\) đi qua điểm \(A\left( { - 1; - 2} \right) \Rightarrow - 2 = a.{\left( { - 1} \right)^2} \Rightarrow a = - 2\)
Tìm các giá trị của \(m \ne \frac{1}{2}\) để hàm số \(y = \left( {2m - 1} \right){x^2}\) đạt giá trị lớn nhất bằng \(0\) tại \(x = 0\).
Ta thấy hàm số \(y = \left( {2m - 1} \right){x^2}\,\,\left( {m \ne \dfrac{1}{2}} \right)\) đạt giá trị lớn nhất bằng \(0\) tại \(x = 0\)
\( \Leftrightarrow 2m - 1 < 0 \Leftrightarrow m < \dfrac{1}{2}\)
Vậy \(m < \dfrac{1}{2}\) thỏa mãn bài toán.
Cho biết quãng đường đi được của một chiếc xe khách được xác định bởi hàm số: \(S = 54t + 2{t^2}\) ( trong đó S là quãng đường đi được tính bằng đơn vị km, t là thời gian xe chuyển động tính bằng đơn vị giờ). Giả sử lúc 9h sáng xe đang ở bến xe Miền Đông. Hỏi lúc 1h15phút chiều khoảng cách từ xe khách đến bến xe Miền Đông là bao nhiêu? (cho rằng xe khách đi thẳng từ bến xe Miền Đông đi quốc lộ 13 và xe đi không nghỉ)
1h15 phút chiều tức là lúc 13h15 phút Thời gian xe khách đã đi (tính từ bến xe Miền Đông):
t = 13h15 phút - 9h = 4h 15 phút = 4,25 h
Quãng đường mà xe khách đã đi được:
\(S = 54.4,25 + 2.4,{25^2} = 265,625km\)
Vậy: Vào lúc 1h15phút chiều thì khoảng cách từ xe khách đến bến xe Miền Đông là: 265,625km.
Cho hàm số \(y=f\left( x \right)=a{{x}^{2}}\) có đồ thị \(\left( P \right)\) đi qua \(A\left( -3;\dfrac{9}{4} \right)\). Tính \(x\) nếu \(f\left( x \right)=8\).
Có đồ thị \(\left( P \right)\) đi qua \(A\left( -3;\dfrac{9}{4} \right)\) nên toạ độ điểm \(A\) thoả mãn phương trình hàm số.
Ta có :
\(\begin{array}{l}\dfrac{9}{4} = a.{\left( { - 3} \right)^2} \Rightarrow a = \frac{1}{4} \Rightarrow y = f\left( x \right) = \dfrac{1}{4}{x^2} \\f\left( x \right) = 8 \Rightarrow \dfrac{1}{4}{x^2} = 8 \Rightarrow {x^2} = 32 \Rightarrow \left[ \begin{array}{l}x = 4\sqrt 2 \\x = - 4\sqrt 2 \end{array} \right.\end{array}\)
Tìm tọa độ giao điểm của đồ thị hai hàm số \(y = - {x^2}\) và \(y = x - 2\)
Xét phương trình hoành độ giao điểm của hai đồ thị hàm số, ta có:
\(\begin{array}{l} - {x^2} = x - 2\\ \Leftrightarrow {x^2} + x - 2 = 0\\ \Leftrightarrow {x^2} + 2x - x - 2 = 0\\ \Leftrightarrow x\left( {x + 2} \right) - \left( {x + 2} \right) = 0\\ \Leftrightarrow \left( {x - 1} \right)\left( {x + 2} \right) = 0\\ \Leftrightarrow \left[ \begin{array}{l}x - 1 = 0\\x + 2 = 0\end{array} \right. \Leftrightarrow \left[ \begin{array}{l}x = 1\\x = - 2\end{array} \right.\end{array}\)
Với \(x = 1 \Rightarrow y = - {1^2} = - 1\)
Với \(x = - 2 \Rightarrow y = - {\left( { - 2} \right)^2} = - 4\)
Vậy tọa độ giao điểm cần tìm là \(\left( {1; - 1} \right),\left( { - 2; - 4} \right).\)
Tìm tất cả các giá trị của \(m\) để đồ thị hàm số \(y = \left( {2m + 1} \right){x^2}\) nằm phía dưới trục hoành.
Đồ thị hàm số \(y = \left( {2m + 1} \right){x^2}\) nằm phía dưới trục hoành tức là \(y < 0 \Leftrightarrow 2m + 1 < 0 \Leftrightarrow m < - \dfrac{1}{2}\,\,\left( {Do\,\,\,{x^2} \ge 0} \right)\)
Đồ thị hàm số \(y = \dfrac{1}{4}{x^2}\) đi qua điểm
Thay \(x = 2\) vào công thức hàm số ta được: \(\dfrac{1}{4}{.2^2} = 1 = {y_Q} \Rightarrow Q\left( {2;1} \right)\) thuộc đồ thị hàm số.
Cho hàm số \(y = a{x^2}\) có đồ thị như hình vẽ bên. Hàm số đó là:
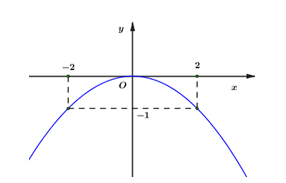
Dựa vào đồ thị hàm số ta thấy đồ thị hàm số đi qua điểm \(\left( {2; - 1} \right)\)\( \Rightarrow - 1 = a{.2^2} \Leftrightarrow a = - \dfrac{1}{4}.\)
\( \Rightarrow y = - \dfrac{1}{4}{x^2}.\)
Đồ thị trong hình bên là của hàm số:
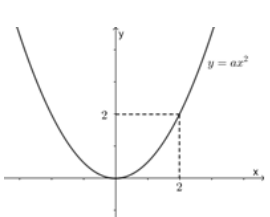
Điểm \(\left( {2;2} \right)\) thuộc đồ thị hàm số \(y = a{x^2}\) nên \(2 = a{.2^2} \Rightarrow a = \dfrac{1}{2}\)
Vậy \(y=\dfrac{1}{2}x^2\)
Tìm \(m\) để đồ thị hàm số \(y = \left( {m + 5} \right){x^2}\) đi qua điểm \(A\left( { - 1;\,\,2} \right).\)
\(A\left( { - 1;\,\,2} \right)\) thuộc đồ thị hàm số \(y = \left( {m + 5} \right){x^2} \Rightarrow 2 = \left( {m + 5} \right).{\left( { - 1} \right)^2} \Leftrightarrow m + 5 = 2 \Leftrightarrow m = - 3.\)
Tìm \(m\) để đồ thị hàm số \(y = \left( {2m + 1} \right){x^2}\) đi qua điểm \(A\left( {1;5} \right)\).
Vì đồ thị hàm số \(y = \left( {2m + 1} \right){x^2}\) đi qua điểm \(A\left( {1;5} \right)\)nên ta có:
\(\begin{array}{l}5 = \left( {2m + 1} \right){.1^2}\\ \Rightarrow 5 = 2m + 1\\ \Rightarrow m = 2\end{array}\)
Vậy với \(m = 2\) đồ thị hàm số \(y = \left( {2m + 1} \right){x^2}\) đi qua điểm \(A\left( {1;5} \right)\)
Cho hàm số \(y=(2-\sqrt{m-1}){{x}^{2}}\). Tìm \(m\) để đồ thị hàm số đi qua điểm \(\left( 2;2 \right)\)
Điều kiện: \(m\ge 1\)
Đồ thị hàm số đi qua điểm \(\left( 2;2 \right)\) nên toạ độ của nó phải thoả mãn phương trình \(y=(2-\sqrt{m-1}){{x}^{2}}\).
Ta có \(2=(2-\sqrt{m-1}){{.2}^{2}}\Leftrightarrow (2-\sqrt{m-1})=\dfrac{1}{2}\)\(\Rightarrow \sqrt{m-1}=\dfrac{3}{2}\)\(\Rightarrow m-1=\dfrac{9}{4}\)\(\Rightarrow m=\dfrac{13}{4}\) (thỏa mãn)

