Tìm toạ độ giao điểm của đồ thị \(\left( P \right)\) của hàm số \(y=\left( m-1 \right){{x}^{2}}\) với đường thẳng \(d:y=2x-1\) biết \(\left( P \right)\) đi qua điểm \(\left( 2;4 \right)\)
Đồ thị \(\left( P \right)\) của hàm số \(y=\left( m-1 \right){{x}^{2}}\) đi qua điểm \(\left( 2;4 \right)\) nên ta có \(4=(m-1){{.2}^{2}}\Leftrightarrow 1=m-1\Leftrightarrow m=2\).
Vậy \(\left( P \right):y={{x}^{2}}\). Hoành độ giao điểm của \(d\) và \(\left( P \right)\) là nghiệm của phương trình:\({{x}^{2}}-(2x-1)=0\Leftrightarrow {{(x-1)}^{2}}=0\Leftrightarrow x=1\)\(\Rightarrow y=1\)
Vậy \(d\) giao với \(\left( P \right)\) tại điểm \(\left( 1;1 \right)\).
Trên một hệ trục toạ độ, vẽ parabol \(\left( P \right)\) có đỉnh \(O\) và đi qua \(A\left( \sqrt{3};-3 \right)\). Hoành độ điểm thuộc \(\left( P \right)\) có tung độ bằng \(-2\) là:
Vì parabol có đỉnh \(O\) nên có dạng \(y=a{{x}^{2}}\left( a\ne 0 \right)\).
\(\left( P \right)\) đi qua \(A\left( \sqrt{3};-3 \right)\) nên toạ độ điểm \(A\) thoả mãn phương trình hàm số.
Ta có \(-3=a{{(\sqrt{3})}^{2}}\Rightarrow a=-1\Rightarrow y=-{{x}^{2}}\).
Thay \(y=-2\) vào hàm số ta được \(-2=-{{x}^{2}}\Rightarrow {{x}^{2}}=2\Rightarrow \left[\begin{align} & x=\sqrt{2} \\ & x=-\sqrt{2} \\\end{align} \right.\)
Cho hàm số \(y=\dfrac{25}{4}{{x}^{2}}\). Xác định toạ độ điểm \(A\) thuộc đồ thị hàm số và có tung độ là \(1\).
Điểm \(A\) có tung độ là \(1\) nên thay \(y=1\) vào phương trình \(y=\dfrac{25}{4}{{x}^{2}}\) ta được \(x=\dfrac{2}{5}\) hoặc \(x=-\dfrac{2}{5}\).
Vậy \(A\left( \dfrac{2}{5};1 \right)\) hoặc \(A\left( -\dfrac{2}{5};1 \right)\)
Cho hàm số $y = a{x^2}\,\,$ với $a \ne 0$. Kết luận nào sau đây là đúng?
Cho hàm số $y = {\rm{a}}{{\rm{x}}^2}\,\,(a \ne 0)$.
a) Nếu $a > 0$ thì hàm số nghịch biến khi $x < 0$ và đồng biến khi $x > 0$.
b) Nếu $a < 0$ thì hàm số đồng biến khi $x < 0$ và nghịch biến khi $x > 0$.
Kết luận nào sau đây là sai khi nói về đồ thị của hàm số $y = a{x^2}\,\,$ với $a \ne 0$.
Đồ thị của hàm số \(y = a{x^2}\left( {a \ne 0} \right)\) là một parabol đi qua gốc tọa độ $O,$ nhận $Oy$ là trục đối xứng ($O$ là đỉnh của parabol).
- Nếu \(a > 0\) thì đồ thị nằm phía trên trục hoành, $O$ là điểm thấp nhất của đồ thị.
- Nếu \(a < 0\) thì đồ thị nằm phía dưới trục hoành, $O$ là điểm cao nhất của đồ thị.
Giá trị của hàm số $y = f\left( x \right) = - 7{x^2}$ tại ${x_0} = - 2$ là
Thay ${x_0} = - 2$ vào hàm số $y = f\left( x \right) = - 7{x^2}$ ta được $f\left( { - 2} \right) = - 7.{\left( { - 2} \right)^2} = - 28$
Cho hàm số $y = f\left( x \right) = \left( { - 2m + 1} \right){x^2}.$
Tìm giá trị của $m$ để đồ thị đi qua điểm $A\left( { - 2;4} \right).$
Thay tọa độ điểm $A\left( { - 2;4} \right)$ vào hàm số $y = f\left( x \right) = \left( { - 2m + 1} \right){x^2}$ ta được
$\left( { - 2m + 1} \right).{\left( { - 2} \right)^2} = 4 \Leftrightarrow - 2m + 1 = 1 \Leftrightarrow m = 0$
Vậy $m = 0$ là giá trị cần tìm.
Cho hàm số \(y = f\left( x \right) = - 2{x^2}\) . Tổng các giá trị của $a$ thỏa mãn $f\left( a \right) = - 8 + 4\sqrt 3 $ là
Ta có $f\left( a \right) = - 8 + 4\sqrt 3 $$ \Leftrightarrow - 2{a^2} = - 8 + 4\sqrt 3 $$ \Leftrightarrow {a^2} = 4 - 2\sqrt 3 $$ \Leftrightarrow {a^2} = {\left( {\sqrt 3 - 1} \right)^2}$
$ \Leftrightarrow \left[ \begin{array}{l}a = \sqrt 3 - 1\\a = 1 - \sqrt 3 \end{array} \right.$
Vậy tổn các giá trị của $a$ là $\left( {\sqrt 3 - 1} \right) + \left( {1 - \sqrt 3 } \right) = 0$
Cho hàm số \(y = \left( {5m + 2} \right){x^2}\) với $m \ne - \dfrac{2}{5}$. Tìm $m$ để hàm số nghịch biến với mọi \(x > 0.\)
Để hàm số nghịch biến với mọi \(x > 0\) thì $a < 0$ nên $5m + 2 < 0 \Leftrightarrow m < - \dfrac{2}{5}$.
Vậy $m < - \dfrac{2}{5}$ thỏa mãn điều kiện đề bài.
Cho hàm số \(y = \left( {4 - 3m} \right){x^2}\) với $m \ne \dfrac{4}{3}$. Tìm $m$ để hàm số đồng biến với mọi \(x > 0\)
Để hàm số đồng biến với mọi \(x > 0\) thì $a > 0$ nên $4 - 3m > 0 \Leftrightarrow 4>3m$$ \Leftrightarrow 3m<4\Leftrightarrow m < \dfrac{4}{3}$.
Vậy $m < \dfrac{4}{3}$ thỏa mãn điều kiện đề bài
Trong các điểm $A(1;2);B( - 1; - 1);C(10; - 200);D\left( {\sqrt {10} ; - 10} \right)$ có bao nhiêu điểm thuộc đồ thị hàm số $\left( P \right): y = - {x^2}$
+) Thay tọa độ điểm $A\left( {1;2} \right)$ vào hàm số $y = - {x^2}$ ta được $2 = - {1^2}$( vô lý) nên $A \notin \left( P \right)$
+) Thay tọa độ điểm $C\left( {10; - 200} \right)$ vào hàm số $y = - {x^2}$ ta được $ - 200 = - {\left( {10} \right)^2} \Leftrightarrow - 200 = - 100$( vô lý) nên loại $C \notin \left( P \right)$
+) Thay tọa độ điểm $D\left( {\sqrt {10} ; - 10} \right)$ vào hàm số $y = - {x^2}$ ta được $ - 10 = - {\left( {\sqrt {10} } \right)^2} \Leftrightarrow - 10 = - 10$( luôn đúng) nên $D \in \left( P \right)$
+) Thay tọa độ điểm $B\left( { - 1; - 1} \right)$ vào hàm số $y = - {x^2}$ ta được $ - 1 = - {\left( { - 1} \right)^2} \Leftrightarrow - 1 = - 1$ (luôn đúng)
$B \in \left( P \right)$.
Cho hàm số \(y = f\left( x \right) = 3{x^2}\). Tìm $b$ biết \(f\left( b \right) \ge 6b + 9\).
Ta có \(f\left( b \right) \ge 6b + 9\) $ \Leftrightarrow 3{b^2} \ge 6b + 9 \Leftrightarrow {b^2} - 2b - 3 \ge 0$$ \Leftrightarrow \left( {b + 1} \right)\left( {b - 3} \right) \ge 0 $
\(\begin{array}{l}
TH1:\left\{ \begin{array}{l}
b + 1 \ge 0\\
b - 3 \ge 0
\end{array} \right. \Leftrightarrow \left\{ \begin{array}{l}
b \ge - 1\\
b \ge 3
\end{array} \right. \Rightarrow b \ge 3\\
TH2:\left\{ \begin{array}{l}
b + 1 \le 0\\
b - 3 \le 0
\end{array} \right. \Leftrightarrow \left\{ \begin{array}{l}
b \le - 1\\
b \le 3
\end{array} \right. \Rightarrow b \le - 1
\end{array}\)
Vậy $\left[ \begin{array}{l}b \le - 1\\b \ge 3\end{array} \right.$ là giá trị cần tìm.
Cho hàm số \(y = \left( {2m + 2} \right){x^2}\). Tìm $m$ để đồ thị hàm số đi qua điểm $A\left( {x;y} \right)$ với $\left( {x;y} \right)$ là nghiệm của hệ phương trình \(\left\{ \begin{array}{l}x - y = 1\\2x - y = 3\end{array} \right.\)
Ta có \(\left\{ \begin{array}{l}x - y = 1\\2x - y = 3\end{array} \right.\)$ \Leftrightarrow \left\{ \begin{array}{l}x = y + 1\\2\left( {y + 1} \right) - y = 3\end{array} \right. \Leftrightarrow \left\{ \begin{array}{l}x = 2\\y = 1\end{array} \right.$$ \Rightarrow A\left( {2;1} \right)$
Thay $x = 2;y = 1$ vào hàm số \(y = \left( {2m + 2} \right){x^2}\) ta được
$1 = \left( {2m + 2} \right){.2^2} \Leftrightarrow 2m + 2 = \dfrac{1}{4} \Leftrightarrow 2m = \dfrac{{ - 7}}{4} \Leftrightarrow m = \dfrac{{ - 7}}{8}$
Vậy $m = - \dfrac{7}{8}$ là giá trị cần tìm.
Cho hàm số \(y = \left( { - {m^2} + 4m - 5} \right){x^2}\) . Kết luận nào sau đây là đúng
Ta thấy hàm số \(y = \left( { - {m^2} + 4m - 5} \right){x^2}\) có
$a = - {m^2} + 4m - 5 = - \left( {{m^2} - 4m + 4} \right) - 1 = - {\left( {m - 2} \right)^2} - 1$
Vì \((m-2)^2\ge 0\) với mọi \(m\) nên \(-(m-2)^2\le 0\) với mọi m
Suy ra \(-(m-2)^2-1\le 0-1\Rightarrow -(m-2)^2-1\le -1<0\) với mọi m
Hay \(a<0\) với mọi m
Nên hàm số đồng biến khi \(x < 0\) và nghịch biến khi \(x > 0\). Suy ra C,D sai.
Và đồ thị hàm số nằm phía dưới trục hoành, O là điểm cao nhất của đồ thị.
Suy ra A sai.
Hình vẽ dưới đây là của đồ thị hàm số nào?
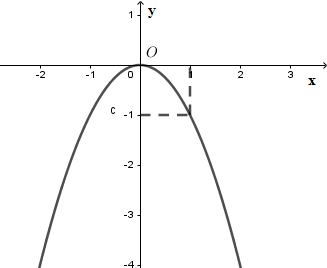
Từ hình vẽ suy ra $a < 0$ nên loại B,C
Vì đồ thị đi qua điểm có tọa độ $\left( {1; - 1} \right)$ nên loại D.
Cho hàm số $y = \sqrt 3 {x^2}\,\,$có đồ thị là $(P)$. Có bao nhiêu điểm trên $\left( P \right)$ có tung độ gấp đôi hoành độ.
Gọi điểm $M$$\left( {x;y} \right)$ là điểm cần tìm. Vì $M$ có tung độ gấp đôi hoành độ nên $M\left( {x;2x} \right)$.
Thay tọa độ điểm $M$ vào hàm số ta được
$2x = \sqrt 3 {x^2} \Leftrightarrow \left[ \begin{array}{l}x = 0 \Rightarrow y = 0\\x = \dfrac{{2\sqrt 3 }}{3} \Rightarrow y = \dfrac{{4\sqrt 3 }}{3}\end{array} \right.$
Hay có hai điểm thỏa mãn điều kiện là $O\left( {0;0} \right),M\left( {\dfrac{{2\sqrt 3 }}{3};\dfrac{{4\sqrt 3 }}{3}} \right)$.
Cho $(P):y = \dfrac{1}{2}{x^2};(d):y = x - \dfrac{1}{2}$. Tìm toạ độ giao điểm của $(P)$ và $(d)$.
Xét phương trình hoành độ giao điểm của parabol $\left( P \right)$ và đường thẳng $d$
$\dfrac{1}{2}{x^2} = x - \dfrac{1}{2} \Leftrightarrow {x^2} - 2x + 1 = 0 \Leftrightarrow {\left( {x - 1} \right)^2} = 0 $$\Leftrightarrow x-1=0\Leftrightarrow x = 1$
Thay \(x=1\) vào hàm số \(y=\dfrac{1}{2}x^2\) ta được \( y = \dfrac{1}{2}.1^2=\dfrac{1}{2}\)
Nên tọa độ giao điểm cần tìm là $\left( {1;\dfrac{1}{2}} \right)$.
Cho parabol \(y = \dfrac{1}{4}{x^2}\). Xác định \(m\) để điểm \(A\left( {\sqrt 2 ;m} \right)\) nằm trên parabol.
Thay \(x = \sqrt 2 ;y = m\) vào hàm số \(y = \dfrac{1}{4}{x^2}\) ta được \(m = \dfrac{1}{4}.{\left( {\sqrt 2 } \right)^2} = \dfrac{1}{2}.\)
Vậy \(m = \dfrac{1}{2}.\)
Cho parabol$(P):y = 2{x^2}$ và đường thẳng $(d):y = x + 1$. Số giao điểm của đường thẳng $d$ và parabol $\left( P \right)$ là:
Xét phương trình hoành độ giao điểm của parabol $\left( P \right)$ và đường thẳng $d$
$2{x^2} = x + 1 \Leftrightarrow 2{x^2} - x - 1 = 0 \\\Leftrightarrow 2{x^2} - 2x + x - 1 = 0 \\\Leftrightarrow 2x\left( {x - 1} \right) + \left( {x - 1} \right) = 0\\ \Leftrightarrow \left( {2x + 1} \right)\left( {x - 1} \right) = 0$
$ \Leftrightarrow \left[ \begin{array}{l}x = - \dfrac{1}{2}\\x = 1\end{array} \right.$
Vậy có hai giao điểm của đường thẳng $d$ và parabol $\left( P \right)$.
Cho parabol $(P):y = \left( {m - 1} \right){x^2}$ và đường thẳng $(d):y = 3 - 2x$. Tìm $m$ để đường thẳng $d$ cắt $\left( P \right)$ tại điểm có tung độ $y = 5$.
Thay $y = 5$ vào phương trình đường thẳng $d$ ta được $5 = 3 - 2x \Leftrightarrow x = - 1$
Nên tọa độ giao điểm của đường thẳng $d$ và parabol $\left( P \right)$ là $\left( { - 1;5} \right)$
Thay $x = - 1;y = 5$ vào hàm số $y = \left( {m - 1} \right){x^2}$ ta được
$\left( {m - 1} \right).{\left( { - 1} \right)^2} = 5 \Leftrightarrow m - 1 = 5 \Leftrightarrow m = 6$
Vậy $m = 6$ là giá trị cần tìm.

