Cho parabol $(P):y = \left( {\dfrac{{1 - 2m}}{2}} \right){x^2}$ và đường thẳng $(d):y = 2x + 2$. Biết đường thẳng $d$ cắt $\left( P \right)$ tại một điểm có tung độ $y = 4$. Tìm hoành độ giao điểm còn lại của $d$ và parabol $\left( P \right)$.
Thay $y = 4$ vào phương trình đường thẳng $d$ ta được $2x + 2 = 4 \Leftrightarrow x = 1$
Nên tọa độ giao điểm của đường thẳng $d$ và parabol $\left( P \right)$ là $\left( {1;4} \right)$
Thay $x = 1;y = 4$ vào hàm số $y = \left( {\dfrac{{1 - 2m}}{2}} \right){x^2}$ ta được
$\dfrac{{1 - 2m}}{2}{.1^2} = 4 \Leftrightarrow 1 - 2m = 8 \Leftrightarrow m = - \dfrac{7}{2}$$ \Rightarrow \left( P \right):y = 4{x^2}$
Xét phương trình hoành độ giao điểm của $d$ và $\left( P \right)$ :
$4{x^2} = 2x + 2 \Leftrightarrow 2{x^2} - x - 1 = 0 \Leftrightarrow \left( {2x + 1} \right)\left( {x - 1} \right) = 0 \Leftrightarrow \left[ \begin{array}{l}x = 1\\x = - \dfrac{1}{2}\end{array} \right.$
Vậy hoành độ giao điểm còn lại là $x = - \dfrac{1}{2}$.
Cho đồ thị hàm số $y = 2{x^2}$$\left( P \right)$ như hình vẽ. Dựa vào đồ thị, tìm $m$ để phương trình $2{x^2} - m - 5 = 0$ có hai nghiệm phân biệt.
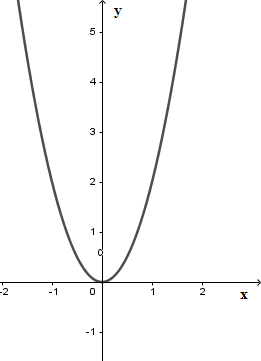
Ta có $2{x^2} - m - 5 = 0$ (*) $ \Leftrightarrow 2{x^2} = m + 5$
Số nghiệm của phương trình (*) là số giao điểm của parabol $\left( P \right):y = 2{x^2}$ và đường thẳng $d:y = m + 5$.
Để (*) có hai nghiệm phân biệt thì $d$ cắt $\left( P \right)$ tại hai điểm phân biệt. Từ đồ thị hàm số ta thấy
Với $m + 5 > 0 \Leftrightarrow m > - 5$ thì $d$ cắt $\left( P \right)$ tại hai điểm phân biệt hay phương trình (*) có hai nghiệm phân biệt khi $m > - 5$.
Lực \(F\) của gió thổi vuông góc vào cánh buồm tỉ lệ thuận với bình phương vận tốc \(v\) của gióm tức là: \(F = a{v^2}\) với \(a\) là hằng số. Biết rằng khi vận tốc của gió là \(2,5m/s\) thì lực tác động lên cánh buồm là \(150N.\) Biết thuyền buồm vẫn có thể đi được nếu vận tốc gió lớn nhất là \(90km/h.\) Tính áp lực lớn nhất mà cánh buồm có thể chịu được.
Theo đề bài ta có: vận tốc của gió là \(2,5m/s\) thì lực tác động lên cánh buồm là \(150N\)
\( \Rightarrow 150 = a.2,{5^2} \Leftrightarrow a = 24\,\,\left( {N{s^2}/{m^2}} \right).\)
Khi đó ta có: \(F = 24{v^2}.\)
Đổi: \({v_{\max }} = 90km/h = \dfrac{{90.1000}}{{3600}} = 25\,\,m/s.\)
Như vậy áp lực lớn nhất mà thuyền buồm có thể chịu được là:
\({F_{\max }} = 24v_{\max }^2 = {24.25^2} = 15000\,\,N.\)
Giá trị nhỏ nhất của hàm số \(y = - 2{x^2}\) khi \(x \in \left[ { - 3;\,\,5} \right]\) là:
Ta có: \(y = - 2{x^2}\) có \(a = - 2 < 0 \Rightarrow \) đồ thị hàm số có bề lõm hướng xuống dưới.
Và hàm số đồng biến khi \(x < 0,\) hàm số nghịch biến khi \(x > 0.\)
+) Với \( - 3 \le x < 0\) ta có: \(y\left( { - 3} \right) \le y\left( x \right) < y\left( 0 \right) \Leftrightarrow - 18 \le y\left( x \right) < 0.\)
+) Với \(0 \le x \le 5\) ta có: \(y\left( 0 \right) \ge y\left( x \right) \ge y\left( 5 \right) \Leftrightarrow 0 \ge y\left( x \right) \ge - 50\)
\( \Rightarrow \) Với mọi \(x \in \left[ { - 3;\,\,5} \right]\) ta có: \( - 50 \le y\left( x \right) \le 0\)
Vậy \(\mathop {Min}\limits_{\left[ { - 3;\,\,5} \right]} y = y\left( { - 5} \right) = - 50.\)
Tìm tất cả các giá trị của tham số \(m\) để đường thẳng \(y = x + 3 - m\) cắt parabol \(y = {x^2}\) tại hai điểm phân biệt.
Xét phương trình hoành độ giao điểm của đường thẳng \(d:\,\,\,y = x + 3 - m\) và parabol \(\left( P \right):\,\,y = {x^2}\) ta có:
\({x^2} = x + 3 - m\) \( \Leftrightarrow {x^2} - x + m - 3 = 0\,\,\,\,\left( * \right)\)
Đường thẳng \(\left( d \right)\) cắt \(\left( P \right)\) tại hai điểm phân biệt \( \Leftrightarrow \left( * \right)\) có hai nghiệm phân biệt
\(\begin{array}{l} \Leftrightarrow \Delta > 0 \Leftrightarrow 1 - 4\left( {m - 3} \right) > 0\\ \Leftrightarrow 1 - 4m + 12 > 0\\ \Leftrightarrow 4m < 13 \Leftrightarrow m < \dfrac{{13}}{4}.\end{array}\)
Vậy \(m < \dfrac{{13}}{4}\) thỏa mãn bài toán.
Cổng vào một ngôi biệt thự có hình dạng là một parabol được biểu diễn bởi đồ thị hàm số \(y = - {x^2}.\) Biết khoảng cách giữa hai chân cổng là \(4\,m.\) Một chiếc ô tô tải có thùng xe là một hình hộp chữ nhật có chiều rộng là \(2,4\,m.\) Hỏi chiều cao lớn nhất có thể của ô tô là bao nhiêu để ô tô có thể đi qua cổng?
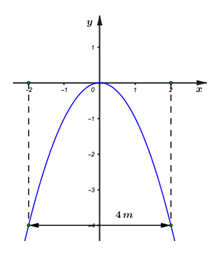
Ta có đồ thị hàm số của cổng biệt thự như hình vẽ.
Khi đó cổng biệt thự có chiều cao \(h = 4\,m.\)
Chiều rộng của thùng xe ô tô tải là \(2,4\,m \Rightarrow {x_0} = \dfrac{1}{2}.2,4 = 1,2m.\)
\( \Rightarrow \) Chiều cao lớn nhất của ô tô tải là: \({h_0} = 1,{2^2} = 1,44m.\)
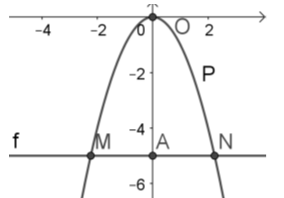
Cho parabol \(y=-{{x}^{2}}\). Vẽ đường thẳng song song với trục hoành cắt trục tung tại điểm \(-5\) và cắt parabol tại \(M\) và \(N\). Diện tích tam giác \(OMN\) là
Đường thẳng song song với \(Ox\) cắt \(Oy\) tại \(-5\) là đường thẳng \(f:y=-5\). Hoành độ giao điểm của \(\left( P \right)\) và \(f\) là nghiệm của phương trình \(-{{x}^{2}}=-5\Rightarrow \left[ \begin{align}& x=\sqrt{5} \\& x=-\sqrt{5} \\\end{align} \right.\). Vậy \(M(-\sqrt{5};-5);N(\sqrt{5};-5)\).
Ta có : \(MN=AM+AN=\left| -\sqrt{5} \right|+\left| \sqrt{5} \right|=2\sqrt{5}\)
\(OA=\left| -5 \right|=5\)
Vậy \({{S}_{OMN}}=\dfrac{1}{2}MN.OA=\dfrac{1}{2}.2\sqrt{5}.5=5\sqrt{5}\).
Cho parabol \(\left( P \right):y=f\left( x \right)={{x}^{2}}\) . Đường thẳng \(d:y=m\) cắt \(\left( P \right)\) tại hai điểm \(A\) và \(B\) sao cho tam giác \(OAB\) đều.
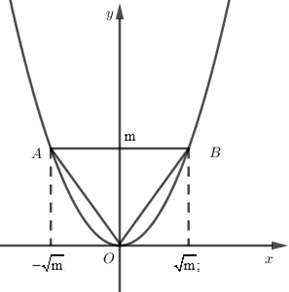
\(\left( P \right)\) cắt \(d\) tại \(2\) điểm phân biệt \(\Leftrightarrow \) phương trình hoành độ giao điểm \({{x}^{2}}-m=0\) phải có hai nghiệm phân biệt suy ra \(m>0\).
Ta có hoành độ của \(A\) và \(B\) là nghiệm của phương trình \({{x}^{2}}=m\Leftrightarrow \left[ \begin{align}& x=\sqrt{m} \\ & x=-\sqrt{m} \\\end{align} \right.\).
Vậy \(A\left( -\sqrt{m};m \right),B\left( \sqrt{m},m \right)\).
Để \(OAB\) là tam giác đều thì \(OA=OB=AB\)
Mà \(OA=\sqrt{{{\left( -\sqrt{m} \right)}^{2}}+{{m}^{2}}},OB=\sqrt{{{\left( \sqrt{m} \right)}^{2}}+{{m}^{2}}}\)
\(AB=\left| -\sqrt{m} \right|+\left| \sqrt{m} \right|=2\sqrt{m}\)
Nên ta có \(\sqrt{{{\left( \sqrt{m} \right)}^{2}}+{{m}^{2}}}=2\sqrt{m}\Leftrightarrow m+{{m}^{2}}=4m\)
\(\Leftrightarrow {{m}^{2}}-3m=0\Leftrightarrow \left[ \begin{align} & m=0 \\ & m=3 \\\end{align} \right.\)
Kết hợp điều kiện \(m>0\) ta được \(m=3\).
Đây là đồ thị của hàm số nào?
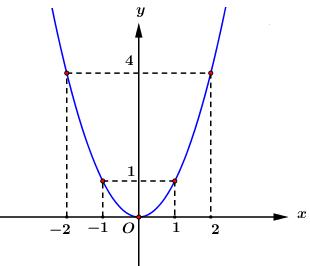
Đồ thi hàm số đi qua điểm (1-;1) và (-1;1) nên quan sát đáp án ta dễ thấy đồ thị trên là đồ thị của hàm số \(y=x^2\)

