Cho parabol \(y=-{{x}^{2}}\). Vẽ đường thẳng song song với trục hoành cắt trục tung tại điểm \(-5\) và cắt parabol tại \(M\) và \(N\). Diện tích tam giác \(OMN\) là
Trả lời bởi giáo viên
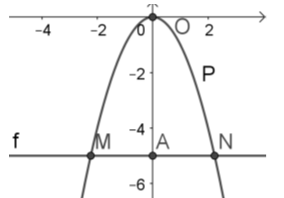
Đường thẳng song song với \(Ox\) cắt \(Oy\) tại \(-5\) là đường thẳng \(f:y=-5\). Hoành độ giao điểm của \(\left( P \right)\) và \(f\) là nghiệm của phương trình \(-{{x}^{2}}=-5\Rightarrow \left[ \begin{align}& x=\sqrt{5} \\& x=-\sqrt{5} \\\end{align} \right.\). Vậy \(M(-\sqrt{5};-5);N(\sqrt{5};-5)\).
Ta có : \(MN=AM+AN=\left| -\sqrt{5} \right|+\left| \sqrt{5} \right|=2\sqrt{5}\)
\(OA=\left| -5 \right|=5\)
Vậy \({{S}_{OMN}}=\dfrac{1}{2}MN.OA=\dfrac{1}{2}.2\sqrt{5}.5=5\sqrt{5}\).
Hướng dẫn giải:
Hoành độ giao điểm hai đồ thị \(y={{f}_{1}}\left( x \right)\) và \(y={{f}_{2}}\left( x \right)\) là nghiệm của phương trình \({{f}_{1}}\left( x \right)-{{f}_{2}}\left( x \right)=0\)
Công thức tính diện tích tam giác: \(S=\frac{1}{2}a.h\) (\(a\) là độ dài đáy, \(h\) là chiều cao tương ứng)

