Câu hỏi:
2 năm trước
Cho parabol \(\left( P \right):y=f\left( x \right)={{x}^{2}}\) . Đường thẳng \(d:y=m\) cắt \(\left( P \right)\) tại hai điểm \(A\) và \(B\) sao cho tam giác \(OAB\) đều.
Trả lời bởi giáo viên
Đáp án đúng: b
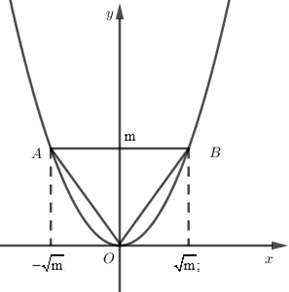
\(\left( P \right)\) cắt \(d\) tại \(2\) điểm phân biệt \(\Leftrightarrow \) phương trình hoành độ giao điểm \({{x}^{2}}-m=0\) phải có hai nghiệm phân biệt suy ra \(m>0\).
Ta có hoành độ của \(A\) và \(B\) là nghiệm của phương trình \({{x}^{2}}=m\Leftrightarrow \left[ \begin{align}& x=\sqrt{m} \\ & x=-\sqrt{m} \\\end{align} \right.\).
Vậy \(A\left( -\sqrt{m};m \right),B\left( \sqrt{m},m \right)\).
Để \(OAB\) là tam giác đều thì \(OA=OB=AB\)
Mà \(OA=\sqrt{{{\left( -\sqrt{m} \right)}^{2}}+{{m}^{2}}},OB=\sqrt{{{\left( \sqrt{m} \right)}^{2}}+{{m}^{2}}}\)
\(AB=\left| -\sqrt{m} \right|+\left| \sqrt{m} \right|=2\sqrt{m}\)
Nên ta có \(\sqrt{{{\left( \sqrt{m} \right)}^{2}}+{{m}^{2}}}=2\sqrt{m}\Leftrightarrow m+{{m}^{2}}=4m\)
\(\Leftrightarrow {{m}^{2}}-3m=0\Leftrightarrow \left[ \begin{align} & m=0 \\ & m=3 \\\end{align} \right.\)
Kết hợp điều kiện \(m>0\) ta được \(m=3\).
Hướng dẫn giải:
Hoành độ giao điểm hai đồ thị \(y={{f}_{1}}\left( x \right)\) và \(y={{f}_{2}}\left( x \right)\) là nghiệm của phương trình \({{f}_{1}}\left( x \right)-\text{ }{{f}_{2}}\left( x \right)=0\)
Hai đồ thị hàm số cắt nhau tại hai điểm phân biệt khi và chỉ khi phương trình hoành độ giao điểm có \(2\) nghiệm phân biệt.
Câu hỏi khác
- Bài tập hàm số bậc hai một ẩn và đồ thị hàm số y=ax^2 toán 9 có lời giải
- Bài tập hệ thức vi-ét và ứng dụng toán 9 có lời giải
- Bài tập phương trình bậc hai một ẩn và công thức nghiệm toán 9 có lời giải
- Bài tập công thức nghiệm thu gọn toán 9 có lời giải
- Bài tập phương trình quy về phương trình bậc hai toán 9 có lời giải
