Cung chứa góc

Quỹ tích các điểm \(M\) nhìn đoạn thẳng \(CD\) cho trước dưới một góc vuông là đường tròn đường kính \(CD.\)

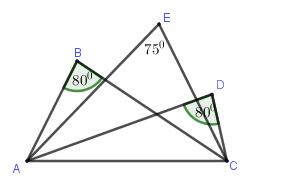
Quan sát hình vẽ ta thấy các điểm \(B,D\) thuộc cung chứa góc \({80^0}\) dựng trên đoạn \(AC\), còn điểm \(E\) thuộc cung chứa góc \({75^0}\) dựng trên đoạn \(AC\).

Do đó chỉ có đáp án \(2\) điểm \(B,D\) cùng thuộc cung chứa góc \({80^0}\) dựng trên đoạn \(AC\) là đúng

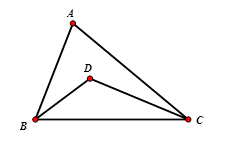
Ta có \(\widehat A = 60^\circ  \Rightarrow \widehat B + \widehat C = 120^\circ \) nên \(\widehat {BDC} + \widehat {DBC} = \dfrac{{120^\circ }}{2} = 60^\circ  \Rightarrow \widehat {BDC} = 120^\circ \)  

 Quỹ tích của điểm D là hai cung chứa góc \(120^0\) dựng trên đoạn BC.

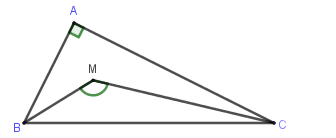
Tam giác ABC có:

\(\widehat A + \widehat B + \widehat C = {180^0}\)  (tính chất tổng 3 góc trong tam giác) $ \Leftrightarrow \widehat B + \widehat C = 90^\circ  \Leftrightarrow \dfrac{1}{2}\widehat B + \dfrac{1}{2}\widehat C = 45^\circ $

Vì M là tâm đường tròn nội tiếp tam giác nên BM, CM là phân giác các góc \(\widehat B,\widehat C\).

Suy ra ta có: \(\widehat {MBC} + \widehat {MCB} = {45^0}\)

 Xét tam giác BMC có: \(\widehat {MBC} + \widehat {MCB} + \widehat {CMB} = {180^0}\)\( \Leftrightarrow \widehat {CMB} = {180^0} - {45^0} = {135^0}\)

* Ta có  B, C cố định \(\widehat {CMB} = {135^0}\)  không đổi

\( \Rightarrow \)   Quỹ tích điểm M là 2 cung chứa góc \({135^0}\)dựng trên BC.

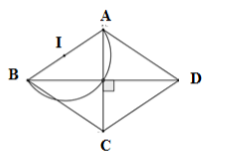
Xét hình vuông $ABCD$ có hai đường chéo $AC$ và $BD$ vuông góc với nhau tại trung điểm của mỗi đường.

Suy ra  \(AO \bot BO \Rightarrow \) \(\widehat {AOB} = {90^\circ }\)

Ta có \(\widehat {AOB} = {90^0}\)   không đổi mà $A,B$ cố định

\( \Rightarrow \)  Quỹ tích điểm $O$ là nửa đường tròn đường kính $AB$ trừ hai điểm $A$ và $B.$

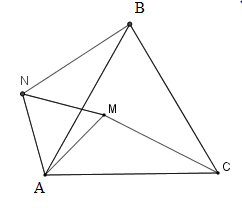
Vẽ tam giác $AMN$ đều ($N$ khác phía $C$ đối với $AM$ ).

Xét \(\Delta BNA\) và \(\Delta AMC\) có:

\(AN = AM\) (vì tam giác $AMN$ đều)

\(BA = BC\) (vì tam giác $ABC$ đều)

\(\widehat {NAB} = \widehat {MAC}\) (vì cùng bằng \({60^\circ } - \widehat {BAM}\) )

Suy ra \(\Delta ANB = \Delta AMC(c.g.c)\) nên ta có $NB = MC$.

Ta có:   \(M{B^2} = M{A^2} + M{C^2} = M{N^2} + N{B^2}\) nên \(\widehat {MNB} = {90^\circ }\). 

Suy ra \(\widehat {BNA} = {90^0} + {60^0} = {150^0}\), do đó \(\widehat {AMC} = \widehat {BNA} = {150^0}\).

$B,C$ cố định

\( \Rightarrow \)  Quỹ tích điểm $M$ là hai cung chứa góc \({150^0}\) dựng trên$AC$ , trừ hai điểm $A$ và$C$ .

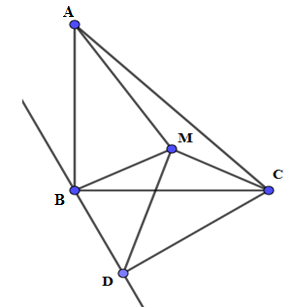
Vẽ tam giác $MBD$ vuông cân tại $B$ ($M$ và $D$ khác phía đối với $BC$ ).

Xét \(\Delta ABM\) và \(\Delta CBD\) có:

\(BM = BD\) (vì tam giác $MBD$ vuông cân tại $B$ )

\(BA = BC\) (vì tam giác $ABC$ vuông cân tại $B$ )

\(\widehat {MBA} = \widehat {CBD}\) (vì cùng bằng \({90^\circ } - \widehat {MBC}\) )

Suy ra \(\Delta ABM = \Delta CBD(c - g - c)\) nên ta có $AM = CD$.

Ta có:  \(2M{B^2} = M{A^2} - M{C^2}\)

\( \Rightarrow 2M{B^2} + M{C^2} = M{A^2} \)\(\Rightarrow {\left( {MB\sqrt 2 } \right)^2} + M{C^2} = C{D^2} \)\(\Rightarrow M{D^2} + M{C^2} = C{D^2}\)

nên \(\widehat {DMC} = {90^0}\).  Suy ra \(\widehat {BMC} = \widehat {BMD} + \widehat {DMC} \)\(= 45^\circ  + 90^\circ  = {135^0}\).  Mà $B,C$ cố định

\( \Rightarrow \) Quỹ tích điểm M là cung chứa góc \({135^0}\) dựng trên $BC$ , trừ hai điểm $B$ và $C$ .

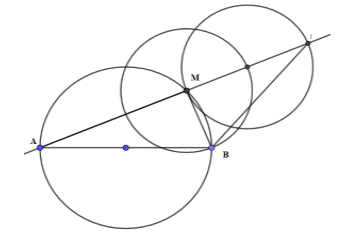
Tam giác $AMB$ vuông tại$M$ , ta có \(\widehat {AMB} = {90^\circ }\). Mặt khác ta có: \(\widehat {AMB} + \widehat {IMB} = {180^\circ },\) suy ra \(\widehat {IMB} = {90^\circ }\)

hay tam giác $BMI$ vuông tại$M$ . Trong tam giác vuông $BMI$ ta có \(tan\widehat {MIB} = \dfrac{{MB}}{{MI}} = \dfrac{2}{3}\)

Suy ra \(\widehat {MIB} = {a^0}\) không đổi hay \(\widehat {AIB} = {a^0}\) không đổi. Mà $A,B$ cố định

\( \Rightarrow \) Quỹ tích điểm $I$ là $2$  cung chứa góc \({a^0}\) dựng trên $AB$ với \(\tan a = \dfrac{2}{3}\)

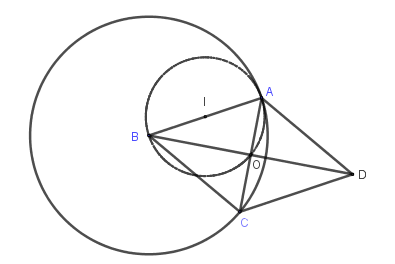
Do \(ABCD\) là hình bình hành có hai cạnh kề bằng nhau nên là hình thoi, do đó hai đường chéo \(AC\) và \(BD\) vuông góc với nhau tại \(O\)

Suy ra  \(AO \bot BO \Rightarrow \) \(\widehat {AOB} = {90^\circ }\)

Ta có \(\widehat {AOB} = {90^0}\)   không đổi, A, B cố định

\( \Rightarrow \)  Quỹ tích điểm O là đường tròn đường kính AB.

Nếu \(C \equiv A\) thì \(O \equiv A\) nên \(A\) thuộc quỹ tích.

Nếu \(C\) đối xứng với \(A\) qua \(B\) thì \(O \equiv B\).

Vậy hai điểm \(A,B\) cũng thuộc quỹ tích         

Quỹ tích các điểm \(M\) nhìn đoạn thẳng \(AB\) cho trước dưới một góc vuông là đường tròn đường kính \(AB\).

Với đoạn thẳng \(AB\) và góc \(\alpha \) \(\left( {0^\circ  < \alpha  < 180^\circ } \right)\) cho trước thì quỹ tích các điểm \(M\) thỏa mãn \(\widehat {AMB} = \alpha \) là hai cung chứa góc \(\alpha \) dựng trên đoạn \(AB\).

Hai cung chứa góc \(\alpha \) nói trên là hai cung tròn đối xứng nhau qua \(AB\). Hai điểm \(A,B\) được coi là thuộc quỹ tích.

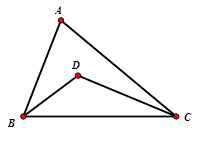
Ta có \(\widehat A = 50^\circ  \Rightarrow \widehat B + \widehat C = 130^\circ \) nên \(\widehat {BDC} + \widehat {DBC} = \dfrac{{130^\circ }}{2} = 65^\circ  \Rightarrow \widehat {BDC} = 115^\circ \)  

Quỹ tích của điểm $D$ là hai cung chứa góc \(115^\circ \) dựng trên đoạn $BC$.

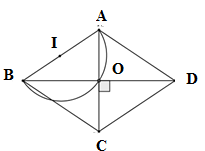
Xét hình thoi $ABCD$ có hai đường chéo $AC$ và $BD$ vuông góc với nhau tại trung điểm của mỗi đường.

Suy ra  \(AO \bot BO \Rightarrow \)  \(\widehat {AOB} = {90^0}\)

Ta có \(\widehat {AOB} = {90^0}\)   không đổi mà $A,B$ cố định

\( \Rightarrow \)  Quỹ tích điểm $O$ là nửa đường tròn đường kính $AB$ trừ hai điểm $A$ và $B.$

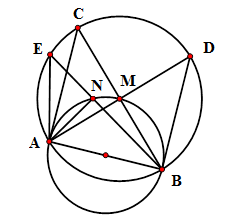
Các tam giác \(\Delta ANE,\,\Delta AMC,\,\Delta BMD\)  lần lượt vuông cân tại $N,M,M$ nên \(\widehat {AEB} = \widehat {ADB} = \widehat {ACB} = 45^\circ \)

Mà $AB$ cố định nên các điểm $A,B,C,D,E$ cùng thuộc một đường tròn.

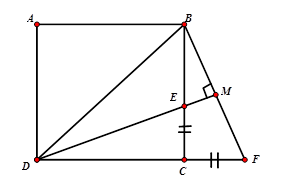
Ta có \(\Delta DEC = \Delta BFC\left( {c - g - c} \right)\) \( \Rightarrow \widehat {EDC} = \widehat {EBM}\) \( \Rightarrow \widehat {EDC} + \widehat {DEC} = \widehat {EBM} + \widehat {BEM} \Rightarrow \widehat {EMB} = 90^\circ \)

Hay \(\widehat {BMD} = 90^\circ \)  nên $M$ thuộc đườngtròn đường kính$BD$ . Mà \(E \in BC\) nên quỹ tích của điểm $M$ là cung \(BC\)  của đường tròn đường kính $BD$ .

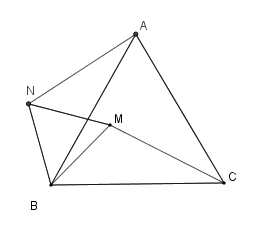
Vẽ tam giác $BMN$ đều ($N$ khác phía $C$ đối với$BM$ ).

Xét \(\Delta BNA\) và \(\Delta BMC\) có:

\(BN = BM\) (vì tam giác $BMN$ đều)

\(BA = BC\) (vì tam giác $ABC$ đều)

\(\widehat {NBA} = \widehat {MBC}\) (vì cùng bằng \({60^0\ } - \widehat {ABM}\) )

Suy ra \(\Delta BNA = \Delta BMC(c.g.c)\) nên ta có $NA = MC$.

Ta có:   \(M{A^2} = M{B^2} + M{C^2} = M{N^2} + N{A^2}\) nên \(\widehat {MNA} = {90^0}\). 

Suy ra \(\widehat {BNA} = {90^0} + {60^0} = {150^0}\), do đó \(\widehat {BMC} = \widehat {BNA} = {150^0}\).

$B,C$ cố định

\( \Rightarrow \)  Quỹ tích điểm $M$ là hai cung chứa góc \({150^0}\) dựng trên$BC$ , trừ hai điểm $B$ và $C$ .

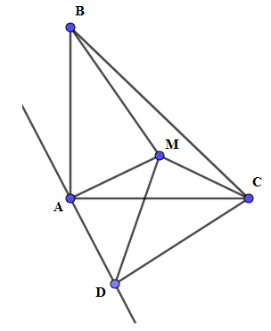
Vẽ tam giác $MAD$ vuông cân tại $A$ ($M$ và $D$ khác phía đối với$AC$ ).

Xét \(\Delta BAM\) và \(\Delta CAD\) có:

\(AM = AD\) (vì tam giác $MAD$ vuông cân tại$A$ )

\(BA = AC\) (vì tam giác $ABC$ vuông cân tại$A$ )

\(\widehat {MAB} = \widehat {CAD}\) (vì cùng bằng \({90^0} - \widehat {MAC}\) )

Suy ra \(\Delta BAM = \Delta CAD(c - g - c)\) nên ta có $BM = CD$.

Ta có:  \(2M{A^2} = M{B^2} - M{C^2}\)

\( \Rightarrow 2M{A^2} + M{C^2} = M{B^2} \Rightarrow {\left( {MA\sqrt 2 } \right)^2} + M{C^2} = C{D^2} \Rightarrow M{D^2} + M{C^2} = C{D^2}\)

nên \(\widehat {DMC} = {90^0}\).  Suy ra \(\widehat {AMC} = {135^0}\).  Mà $A,C$ cố định

\( \Rightarrow \) Quỹ tích điểm M là cung chứa góc \({135^0}\) dựng trên$AC$ , trừ hai điểm $A$ và$C$ .

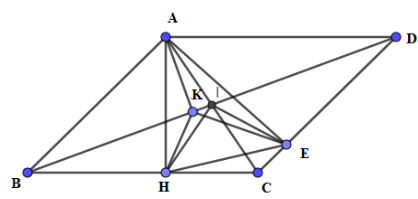
\(AH \bot BC,AE \bot CD \Rightarrow \) bốn điểm $A,H,C,E$ nằm trên đường tròn đường kính$AC$ , $I$ là trung điểm của $AC$

\( \Rightarrow \) $I$ là tâm đường tròn đường kính $AC$

$ \Rightarrow \widehat {HIE} = 2\widehat {HAE} = 2\left( {\widehat {HAC} + \widehat {EAC}} \right)$ \( = 2\left( {{{90}^0} - \widehat {ACB} + {{90}^0} - \widehat {ACE}} \right) = 2\left( {{{180}^0} - \widehat {BCD}} \right)\)

Lại có \(AH \bot BC,AK \bot BD,AE \bot CD\) nên  bốn đỉnh \(A,K,E,D\) nằm trên đường tròn đường kính \(AD\) và  bốn đỉnh \(A;K;H;B\) nằm trên đường tròn đường kính \(AB\) \( \Rightarrow \widehat {EKD} = \widehat {EAD}\) và \(\widehat {BKH} = \widehat {BAH}\)

\( \Rightarrow \widehat {HKE} = {180^0} - \widehat {EKD} - \widehat {BKH} = {180^0} - \widehat {EAD} - \widehat {BAH}\\ = {90^0} - \widehat {EAD} + {90^0} - \widehat {BAH} = \widehat {ADC} + \widehat {ABC} = 2\left( {{{180}^0} - \widehat {BCD}} \right)\)

Suy ra $K$ và $I$ cùng nhìn đoạn $HE$ dưới một góc \(2\left( {{{180}^0} - \widehat {BCD}} \right)\)

Vậy $K,I,E,H$ nằm trên một đường tròn.

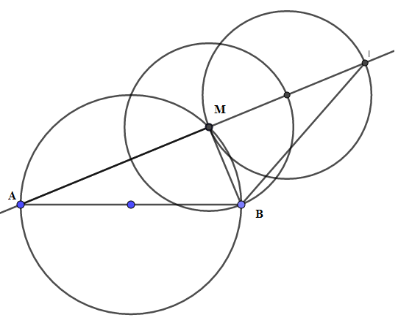
Tam giác $AMB$ vuông tại$M$ , ta có \(\widehat {AMB} = {90^0 }\). Mặt khác ta có: \(\widehat {AMB} + \widehat {IMB} = {180^0 },\) suy ra \(\widehat {IMB} = {90^0 }\)

hay tam giác $BMI$ vuông tại $M$ . Trong tam giác vuông $BMI$ ta có \(\tan\widehat {MIB} = \dfrac{{MB}}{{MI}} = \dfrac{1}{2}\)

Suy ra \(\widehat {MIB} = {a^0}\) không đổi hay \(\widehat {AIB} = {a^0}\) không đổi. Mà $A,B$ cố định

\( \Rightarrow \) Quỹ tích điểm $I$ là $2$  cung chứa góc \({a^0}\) dựng trên $AB$ với \(\tan a = \dfrac{1}{2}.\)

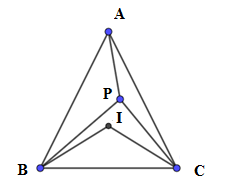
Theo giả thiết ta có:\(\widehat {PBA} + \widehat {PCA} = \widehat {PBC} + \widehat {PCB} \Rightarrow \widehat {PBA} + \widehat {PCA} + \widehat {PBC} + \widehat {PCB} = 2\left( {\widehat {PBC} + \widehat {PCB}} \right)\)

\( \Rightarrow 2\left( {\widehat {PBC} + \widehat {PCB}} \right) = \widehat B + \widehat C \Rightarrow 2\left( {{{180}^0} - \widehat {BPC}} \right) = \widehat B + \widehat C = {180^0} - \widehat {BAC}\)\( \Rightarrow \widehat {BPC} = {90^0} + \dfrac{1}{2}\widehat {BAC}\)

Mặt khác \(\widehat {BIC} = {180^0} - \left( {\widehat {IBC} + \widehat {ICB}} \right) = {180^0} - \dfrac{1}{2}\left( {\widehat {ABC} + \widehat {ACB}} \right)\)

\( = {180^0} - \dfrac{1}{2}\left( {{{180}^0} - \widehat {BAC}} \right) = {90^0} + \dfrac{1}{2}\widehat {BAC}\)

Suy ra $P$ và $I$ luôn nhìn đoạn $BC$ về cùng một phía dưới cùng một góc \({90^0} + \dfrac{1}{2}\widehat {BAC}\).