Câu hỏi:
2 năm trước
Cho các hình vuông $ABCD$ có cạnh $AB$ cố định. Tìm quỹ tích giao điểm $O$ của hai đường chéo của các hình vuông đó.
Trả lời bởi giáo viên
Đáp án đúng: b
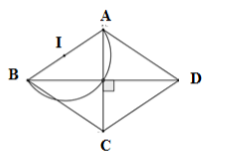
Xét hình vuông $ABCD$ có hai đường chéo $AC$ và $BD$ vuông góc với nhau tại trung điểm của mỗi đường.
Suy ra \(AO \bot BO \Rightarrow \) \(\widehat {AOB} = {90^\circ }\)
Ta có \(\widehat {AOB} = {90^0}\) không đổi mà $A,B$ cố định
\( \Rightarrow \) Quỹ tích điểm $O$ là nửa đường tròn đường kính $AB$ trừ hai điểm $A$ và $B.$
Hướng dẫn giải:
Sử dụng phương pháp cung chứa góc.
Hai điểm $B,C$ cố định. Quỹ tích các điểm $M$ thỏa mãn \(\widehat {BMC} = \alpha \) không đổi là $2$ cung chứa góc \(\alpha \) dựng trên $BC$ .