Câu hỏi:
2 năm trước
Cho tam giác ABC vuông tại A, có cạnh BC cố định. Gọi M là tâm đường tròn nội tiếp tam giác ABC. Tìm quỹ tích điểm M khi A di động.
Trả lời bởi giáo viên
Đáp án đúng: b
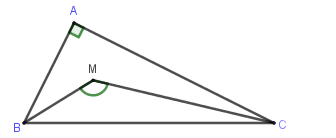
Tam giác ABC có:
\(\widehat A + \widehat B + \widehat C = {180^0}\) (tính chất tổng 3 góc trong tam giác) $ \Leftrightarrow \widehat B + \widehat C = 90^\circ \Leftrightarrow \dfrac{1}{2}\widehat B + \dfrac{1}{2}\widehat C = 45^\circ $
Vì M là tâm đường tròn nội tiếp tam giác nên BM, CM là phân giác các góc \(\widehat B,\widehat C\).
Suy ra ta có: \(\widehat {MBC} + \widehat {MCB} = {45^0}\)
Xét tam giác BMC có: \(\widehat {MBC} + \widehat {MCB} + \widehat {CMB} = {180^0}\)\( \Leftrightarrow \widehat {CMB} = {180^0} - {45^0} = {135^0}\)
* Ta có B, C cố định \(\widehat {CMB} = {135^0}\) không đổi
\( \Rightarrow \) Quỹ tích điểm M là 2 cung chứa góc \({135^0}\)dựng trên BC.
Hướng dẫn giải:
Sử dụng phương pháp cung chứa góc.
Hai điểm B, C cố định. Quỹ tích các điểm M thỏa mãn \(\widehat {BMC} = \alpha \) không đổi là 2 cung chứa góc \(\alpha \) dựng trên BC.
