Câu hỏi:
2 năm trước
Cho tam giác$ABC$ , gọi $I$ là tâm đường tròn nội tiếp tam giác, $P$ là một điểm trong tam giác thỏa mãn \(\widehat {PBA} + \widehat {PCA} = \widehat {PBC} + \widehat {PCB}\). Xét các khẳng định sau:
I. $P$ nhìn đoạn $BC$ dưới một góc \({90^0} + \dfrac{1}{2}\widehat {BAC}\) II. $I$ nhìn đoạn $BC$ dưới một góc \({90^0} + \dfrac{1}{2}\widehat {BAC}\)
Kết luận nào sau đây đúng?
Trả lời bởi giáo viên
Đáp án đúng: b
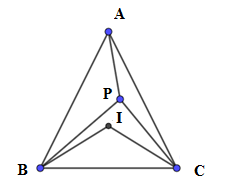
Theo giả thiết ta có:\(\widehat {PBA} + \widehat {PCA} = \widehat {PBC} + \widehat {PCB} \Rightarrow \widehat {PBA} + \widehat {PCA} + \widehat {PBC} + \widehat {PCB} = 2\left( {\widehat {PBC} + \widehat {PCB}} \right)\)
\( \Rightarrow 2\left( {\widehat {PBC} + \widehat {PCB}} \right) = \widehat B + \widehat C \Rightarrow 2\left( {{{180}^0} - \widehat {BPC}} \right) = \widehat B + \widehat C = {180^0} - \widehat {BAC}\)\( \Rightarrow \widehat {BPC} = {90^0} + \dfrac{1}{2}\widehat {BAC}\)
Mặt khác \(\widehat {BIC} = {180^0} - \left( {\widehat {IBC} + \widehat {ICB}} \right) = {180^0} - \dfrac{1}{2}\left( {\widehat {ABC} + \widehat {ACB}} \right)\)
\( = {180^0} - \dfrac{1}{2}\left( {{{180}^0} - \widehat {BAC}} \right) = {90^0} + \dfrac{1}{2}\widehat {BAC}\)
Suy ra $P$ và $I$ luôn nhìn đoạn $BC$ về cùng một phía dưới cùng một góc \({90^0} + \dfrac{1}{2}\widehat {BAC}\).
