Câu hỏi:
3 năm trước
Cho nửa đường tròn đường kính \(AB\). Gọi \(M\) là điểm chính giữa của cung \(AB\) . Trên cung \(AM\) lấy điểm \(N\). Trên tia đối của tia \(MA\) lấy điểm \(D\) sao cho \(MD = MB\), trên tia đối của tia \(NB\) lấy điểm \(E\) sao cho \(NA = NE\), trên tia đối của tia \(MB\) lấy điểm \(C\) sao cho \(MC = MA\) .
Các điểm nào dưới đây cùng thuộc một đường tròn ?
Trả lời bởi giáo viên
Đáp án đúng: c
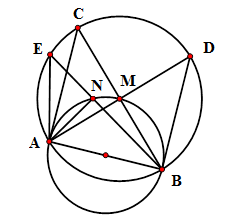
Các tam giác \(\Delta ANE,\,\Delta AMC,\,\Delta BMD\) lần lượt vuông cân tại $N,M,M$ nên \(\widehat {AEB} = \widehat {ADB} = \widehat {ACB} = 45^\circ \)
Mà $AB$ cố định nên các điểm $A,B,C,D,E$ cùng thuộc một đường tròn.
Hướng dẫn giải:
Chứng minh các đỉnh cùng nhìn một đoạn thẳng dưới một góc cho trước