Cho hình vuông \(ABCD\). Trên cạnh \(BC\) lấy điểm \(E\) , trên tia đối của tia \(CD\) lấy điểm \(F\) sao cho \(CE = CF\). Gọi \(M\) là giao điểm của hai đường thẳng \(DE\) và \(BF\). Tìm quỹ tích của điểm \(M\) khi \(E\) di động trên cạnh \(BC\).
Trả lời bởi giáo viên
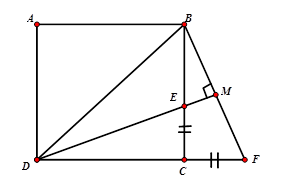
Ta có \(\Delta DEC = \Delta BFC\left( {c - g - c} \right)\) \( \Rightarrow \widehat {EDC} = \widehat {EBM}\) \( \Rightarrow \widehat {EDC} + \widehat {DEC} = \widehat {EBM} + \widehat {BEM} \Rightarrow \widehat {EMB} = 90^\circ \)
Hay \(\widehat {BMD} = 90^\circ \) nên $M$ thuộc đườngtròn đường kính$BD$ . Mà \(E \in BC\) nên quỹ tích của điểm $M$ là cung \(BC\) của đường tròn đường kính $BD$ .
Hướng dẫn giải:
Sử dụng : Quỹ tích các điểm \(M\) nhìn đoạn thẳng \(AB\) cho trước dưới một góc vuông là đường tròn đường kính \(AB\).