Cho tam giác $ABC$ vuông cân tại $A$ . Tìm quỹ tích các điểm $M$ nằm trong tam giác đó sao cho \(2M{A^2} = M{B^2} - M{C^2}\).
Trả lời bởi giáo viên
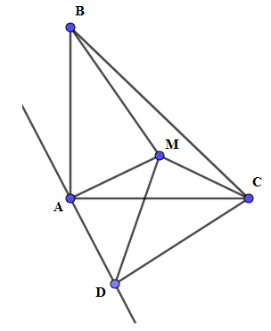
Vẽ tam giác $MAD$ vuông cân tại $A$ ($M$ và $D$ khác phía đối với$AC$ ).
Xét \(\Delta BAM\) và \(\Delta CAD\) có:
\(AM = AD\) (vì tam giác $MAD$ vuông cân tại$A$ )
\(BA = AC\) (vì tam giác $ABC$ vuông cân tại$A$ )
\(\widehat {MAB} = \widehat {CAD}\) (vì cùng bằng \({90^0} - \widehat {MAC}\) )
Suy ra \(\Delta BAM = \Delta CAD(c - g - c)\) nên ta có $BM = CD$.
Ta có: \(2M{A^2} = M{B^2} - M{C^2}\)
\( \Rightarrow 2M{A^2} + M{C^2} = M{B^2} \Rightarrow {\left( {MA\sqrt 2 } \right)^2} + M{C^2} = C{D^2} \Rightarrow M{D^2} + M{C^2} = C{D^2}\)
nên \(\widehat {DMC} = {90^0}\). Suy ra \(\widehat {AMC} = {135^0}\). Mà $A,C$ cố định
\( \Rightarrow \) Quỹ tích điểm M là cung chứa góc \({135^0}\) dựng trên$AC$ , trừ hai điểm $A$ và$C$ .
Hướng dẫn giải:
Sử dụng phương pháp cung chứa góc.
Hai điểm $B,C$ cố định. Quỹ tích các điểm $M$ thỏa mãn \(\widehat {BMC} = \alpha \) không đổi là $2$ cung chứa góc \(\alpha \) dựng trên $BC$ .