Câu hỏi:
2 năm trước
Cho tam giác \(ABC\) có \(BC\) cố định và góc \(A\) bằng \(50^\circ \). Gọi \(D\) là giao điểm của ba đường phân giác trong của tam giác. Tìm quỹ tích điểm \(D\).
Trả lời bởi giáo viên
Đáp án đúng: d
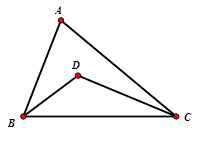
Ta có \(\widehat A = 50^\circ \Rightarrow \widehat B + \widehat C = 130^\circ \) nên \(\widehat {BDC} + \widehat {DBC} = \dfrac{{130^\circ }}{2} = 65^\circ \Rightarrow \widehat {BDC} = 115^\circ \)
Quỹ tích của điểm $D$ là hai cung chứa góc \(115^\circ \) dựng trên đoạn $BC$.
Hướng dẫn giải:
Sử dụng tính chất tia phân giác để tính góc \(BDC\) từ đó sử dụng quỹ tích cung chứa góc