Câu hỏi:
2 năm trước
Cho đoạn thẳng $AB$ cố định và một điểm \(C\) di chuyển trên đường tròn tâm \(B\) bán kính \(BA\). Dựng hình bình hành \(ABCD\). Gọi \(O\) là giao điểm của hai đường chéo hình bình hành. Tìm quỹ tích điểm \(O\) khi \(C\) di chuyển trên đường tròn \(\left( {B;BA} \right)\).
Trả lời bởi giáo viên
Đáp án đúng: b
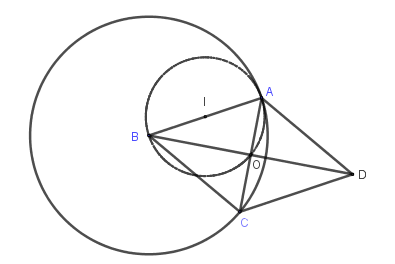
Do \(ABCD\) là hình bình hành có hai cạnh kề bằng nhau nên là hình thoi, do đó hai đường chéo \(AC\) và \(BD\) vuông góc với nhau tại \(O\)
Suy ra \(AO \bot BO \Rightarrow \) \(\widehat {AOB} = {90^\circ }\)
Ta có \(\widehat {AOB} = {90^0}\) không đổi, A, B cố định
\( \Rightarrow \) Quỹ tích điểm O là đường tròn đường kính AB.
Nếu \(C \equiv A\) thì \(O \equiv A\) nên \(A\) thuộc quỹ tích.
Nếu \(C\) đối xứng với \(A\) qua \(B\) thì \(O \equiv B\).
Vậy hai điểm \(A,B\) cũng thuộc quỹ tích
Hướng dẫn giải:
Sử dụng phương pháp cung chứa góc.
Hai điểm B, C cố định. Quỹ tích các điểm M thỏa mãn \(\widehat {BMC} = \alpha \) không đổi là 2 cung chứa góc \(\alpha \) dựng trên BC.
