Hình cầu. Diện tích mặt cầu và thể tích hình cầu

Vì đường kính \(d = 8\,cm\) nên bán kính hình cầu \(R = \dfrac{8}{2} = 4\,\,cm\)

Diện tích mặt cầu \(S = 4\pi {R^2} = 4\pi {.4^2} = 64\pi \,\,\left( {c{m^2}} \right)\)

Ta có \(V = \dfrac{4}{3}\pi {R^3} = 972\pi  \Rightarrow {R^3} = 729 \Rightarrow R = 9\,cm\)

Từ đó đường kính mặt cầu là \(d = 2R = 2.9 = 18\,cm\)

Từ giả thiết ta có \(4\pi {R^2} = 2.\dfrac{4}{3}\pi {R^3} \Rightarrow {R^3} = \dfrac{3}{2}{R^2} \Rightarrow R = \dfrac{3}{2}\)

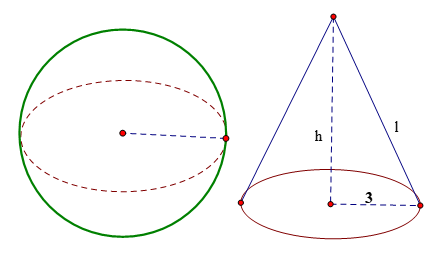
Gọi \(l\) là độ dài đường sinh của hình nón.

Vì bán kính hình cầu và bán kính đáy của hình nón  bằng nhau nên từ giả thiết ta có \(4\pi {R^2} = \pi Rl + \pi {R^2} \Leftrightarrow 4{R^2} = Rl + {R^2} \Leftrightarrow 3{R^2} = Rl \Rightarrow l = 3R = 3.5 = 15\,cm\)

Sử dụng công thức liên hệ trong hình nón ta có \({h^2} = {l^2} - {R^2} = {15^2} - {5^2} = 200 \Rightarrow h = 10\sqrt 2 \,\,cm\)

Vì đường kính đáy và chiều cao của hình trụ bằng nhau và bằng đường kính hình cầu nên \(h = 2R\) với \(R\) là bán kính hình cầu và cũng là bán kính đáy của hình trụ.

Diện tích mặt cầu \(S = 4\pi {R^2}\) , diện tích xung quanh của hình trụ \({S_{xq}} = 2\pi Rh = 2\pi R.2R = 4\pi {R^2}\)

Diện tích toàn phần của hình trụ là \({S_{tp}} = {S_{xq}} + 2\pi {R^2} = 4\pi {R^2} + 2\pi {R^2} = 6\pi {R^2}\)

Tỉ số giữa diện tích mặt cầu và diện tích toàn phần của hình trụ là \(\dfrac{S}{{{S_{tp}}}} = \dfrac{{4\pi {R^2}}}{{6\pi {R^2}}} = \dfrac{2}{3}\) .

Từ đề bài suy ra chiều cao hình trụ là \(h = 3R\) với \(R\) là bán kính hình cầu và cũng là bán kính đáy của hình trụ.

Thể tích hình cầu \({V_c} = \dfrac{4}{3}\pi {R^3}\) ; thể tích khối trụ \({V_t} = \pi {R^2}.3R = 3\pi {R^3}\)

Tỉ số thể tích hình cầu và thể tích hình trụ là \(\dfrac{{{V_c}}}{{{V_t}}} = \dfrac{{\dfrac{4}{3}\pi {R^3}}}{{3\pi {R^3}}} = \dfrac{4}{9}\) .

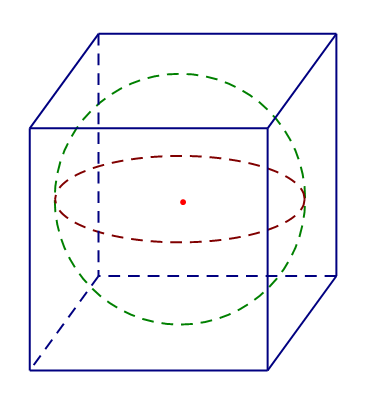
Vì hình cầu nội tiếp hình lập phương nên bán kính hình cầu \(R = \dfrac{a}{2}\)  với \(a\) là cạnh hình lập phương.

Diện tích toàn phần của hình lập phương \({S_{tp}} = 6{a^2} = 24 \Leftrightarrow a = 2cm\)

Suy ra \(R = \dfrac{2}{2} = 1cm\)

Khi đó ta có diện tích mặt cầu \(S = 4\pi {R^2} = 4\pi {.1^2} = 4\pi \left( {c{m^2}} \right)\)

Vì tam giác \(ABC\) vuông tại \(A\) nên  có đường tròn ngoại tiếp là đường tròn đường kính \(BC\) .

Bán kính đường tròn ngoại tiếp tam giác là \(R = \dfrac{{BC}}{2}\)

Theo định lý Pytago ta có \(B{C^2} = A{B^2} + A{C^2} = {2.6^2} \Rightarrow BC = 6\sqrt 2 \)\( \Rightarrow R = \dfrac{{6\sqrt 2 }}{2} = 3\sqrt 2 \)

Khi quay nửa đường tròn ngoại tiếp tam giác \(ABC\) một vòng quanh cạnh \(BC\) ta được hình cầu có bán kính \(R = 3\sqrt 2 \)  nên diện tích mặt cầu là \(S = 4\pi {R^2} = 4\pi {\left( {3\sqrt 2 } \right)^2} = 72\pi \,\left( {c{m^2}} \right)\) .

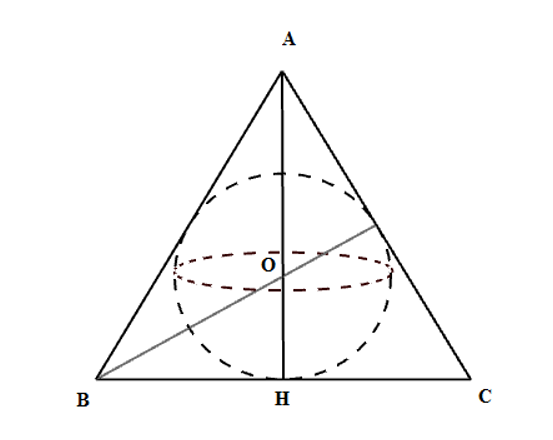
Vì \(\Delta ABC\) là tam giác đều nên tâm đường tròn nội tiếp trùng với trọng tâm \(O\) của tam giác.

Khi đó bán kính đường tròn nội tiếp là \(R = OH = \dfrac{{AH}}{3}\)

Xét tam giác vuông \(ABH\) có \(A{H^2} = A{B^2} - B{H^2} = {12^2} - {\left( {\dfrac{{12}}{2}} \right)^2} = 108 \Rightarrow AH = 6\sqrt 3 \)

Suy ra \(R = \dfrac{{AH}}{3} = 2\sqrt 3 \)

Khi quay nửa đường tròn nội tiếp tam giác \(ABC\) một vòng quanh \(AH\) ta được hình cầu bán kính \(R = 2\sqrt 3 \)\( \Rightarrow V = \dfrac{4}{3}\pi {R^3} = \dfrac{4}{3}\pi .{\left( {2\sqrt 3 } \right)^3} = 32\pi \sqrt 3 \left( {c{m^3}} \right)\)

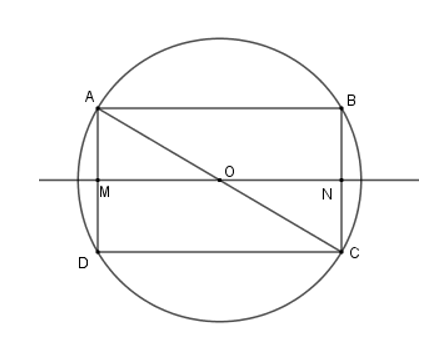
Gọi \(O\) là tâm của hình chữ nhật nên \(OA = OB = OC = OD\) nên \(O\) là tâm đường tròn ngoại tiếp hình chữ nhật \(ABCD\) . Khi đó bán kính đường tròn là \(R = OA = \dfrac{{AC}}{2}\)

Theo định lý Pytago ta có \(A{C^2} = A{D^2} + D{C^2} = {6^2} + {8^2} = 100 \Rightarrow AC = 10\) (vì \(AB = DC = 8\,cm\) )\( \Rightarrow R = 5cm\)

Khi quay nửa đường tròn ngoại tiếp hình chữ nhật \(ABCD\) quay quanh đường thẳng \(MN\) với \(M\) là trung điểm \(AD\) , \(N\) là trung điểm \(BC\) ta được một hình cầu tâm \(O\) bán kính \(R = 5cm\)

Diện tích mặt cầu là \(S = 4\pi {R^2} = 4.\pi {5^2} = 100\pi \) \(\left( {cm} \right)\) .

Vì đường kính \(d = 6\,cm\) nên bán kính hình cầu \(R = \dfrac{6}{2} = 3\,\,cm\)

Diện tích mặt cầu $S = 4\pi {R^2} = 4\pi {.3^2} = 36\pi \,\,\left( {c{m^2}} \right)$

Ta có \(V = \dfrac{4}{3}\pi {R^3} = 288\pi  \Rightarrow {R^3} = 216 \Rightarrow R = 6\,cm\)

Từ đó đường kính mặt cầu là \(d = 2R = 2.6 = 12\,cm\).

Từ giả thiết ta có \(4\pi {R^2} = \dfrac{4}{3}\pi {R^3} \Rightarrow {R^3} = 3{R^2} \Rightarrow R = 3\,\)

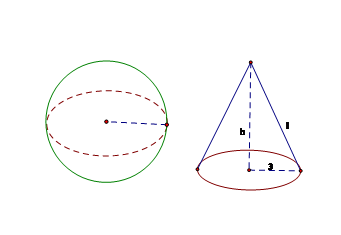
Gọi \(l\) là độ dài đường sinh của hình nón.

Vì bán kính hình cầu và bán kính đáy của hình nón  bằng nhau nên từ giả thiết ta có \(4\pi {R^2} = \pi Rl + \pi {R^2} \Leftrightarrow 4{R^2} = Rl + {R^2} \Leftrightarrow 3{R^2} = Rl \Rightarrow l = 3R = 3.3 = 9\,cm\)

Sử dụng công thức liên hệ trong hình nón ta có \({h^2} = {l^2} - {R^2} = {9^2} - {3^2} = 72 \)

$\Rightarrow h = 6\sqrt 2 \,\,cm$.

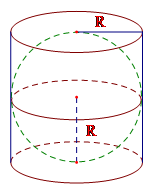
Vì đường kính đáy và chiều cao của hình trụ bằng nhau và bằng đường kính hình cầu nên \(h = 2R\) với \(R\) là bán kính hình cầu và cũng là bán kính đáy của hình trụ.

Diện tích mặt cầu \(S = 4\pi {R^2}\) , diện tích xung quanh của hình trụ \({S_{xq}} = 2\pi Rh = 2\pi R.2R = 4\pi {R^2}\)

Tỉ số giữa diện tích mặt cầu và diện tích xung quanh của hình trụ là \(\dfrac{S}{{{S_{xq}}}} = \dfrac{{4\pi {R^2}}}{{4\pi {R^2}}} = 1\) .

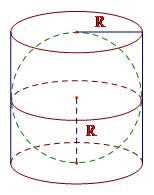
Vì đường kính đáy và chiều cao của hình trụ bằng nhau và bằng đường kính hình cầu nên \(h = 2R\) với \(R\) là bán kính hình cầu và cũng là bán kính đáy của hình trụ.

Thể tích hình cầu \({V_c} = \dfrac{4}{3}\pi {R^3}\) ; thể tích khối trụ ${V_t} = \pi {R^2}.2R = 2\pi {R^3}$

Tỉ số thể tích hình cầu và thể tích hình trụ là \(\dfrac{{{V_c}}}{{{V_t}}} = \dfrac{{\dfrac{4}{3}\pi {R^3}}}{{2\pi {R^3}}} = \dfrac{2}{3}\) .

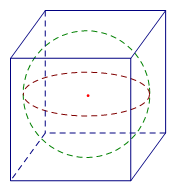
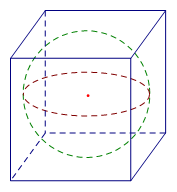
Vì hình cầu nội tiếp hình lập phương nên bán kính hình cầu \(R = \dfrac{a}{2}\)  với \(a\) là cạnh hình lập phương.

Khi đó ta có diện tích mặt cầu \(S = 4\pi {R^2} = 4\pi .{\left( {\dfrac{a}{2}} \right)^2} = \pi {a^2}\)

Diện tích toàn phần của hình lập phương \({S_{tp}} = 6{a^2}\)

Tỉ số giữa diện tích mặt cậu và diện tích toàn phần của hình lập phương là \(\dfrac{S}{{{S_{tp}}}} = \dfrac{{\pi {a^2}}}{{6{a^2}}} = \dfrac{\pi }{6}\)

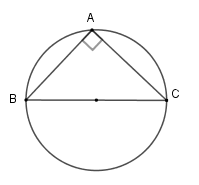
Vì tam giác \(ABC\) vuông tại \(A\) nên  có đường tròn ngoại tiếp là đường tròn đường kính \(BC\) .

Bán kính đường tròn ngoại tiếp tam giác là \(R = \dfrac{{BC}}{2}\)

Theo định lý Pytago ta có \(B{C^2} = A{B^2} + A{C^2} = 2{a^2} \Rightarrow BC = a\sqrt 2 \) \( \Rightarrow R = \dfrac{{a\sqrt 2 }}{2}\)

Khi quay nửa đường tròn ngoại tiếp tam giác $ABC$ một vòng quanh cạnh $BC$ ta được hình cầu có bán kính \(R = \dfrac{{a\sqrt 2 }}{2}\)  nên diện tích mặt cầu là \(S = 4\pi {R^2} = 4\pi {\left( {\dfrac{{a\sqrt 2 }}{2}} \right)^2} = 2\pi {a^2}\) .

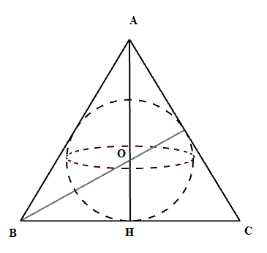
Vì \(\Delta ABC\) là tam giác đều nên tâm đường tròn nội tiếp trùng với trọng tâm \(O\) của tam giác.

Khi đó bán kính đường tròn nội tiếp là \(R = OH = \dfrac{{AH}}{3}\)

Xét tam giác vuông \(ABH\) có \(A{H^2} = A{B^2} - B{H^2} = {a^2} - {\left( {\dfrac{a}{2}} \right)^2} = \dfrac{{3{a^2}}}{4} \Rightarrow AH = \dfrac{{a\sqrt 3 }}{2}\)

Suy ra \(R = \dfrac{{a\sqrt 3 }}{6}\)

Khi quay nửa đường tròn nội tiếp tam giác $ABC$ một vòng quanh $AH$ ta được hình cầu bán kính \(R = \dfrac{{a\sqrt 3 }}{6}\)\( \Rightarrow V = \dfrac{4}{3}\pi {R^3} = \dfrac{4}{3}\pi .{\left( {\dfrac{{a\sqrt 3 }}{6}} \right)^3} = \dfrac{{\sqrt 3 \pi {a^3}}}{{54}}\) 

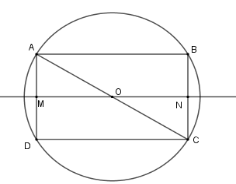
Gọi \(O\) là tâm của hình chữ nhật nên $OA = OB = OC = OD$ nên \(O\) là tâm đường tròn ngoại tiếp hình chữ nhật \(ABCD\) . Khi đó bán kính đường tròn là \(R = OA = \dfrac{{AC}}{2}\)

Theo định lý Pytago ta có \(A{C^2} = A{D^2} + D{C^2} = {3^2} + {4^2} = 25 \Rightarrow AC = 5\) (vì \(AB = DC = 4\,cm\) )\( \Rightarrow R = \dfrac{5}{2}\)

Khi quay nửa đường tròn ngoại tiếp hình chữ nhật \(ABCD\) quay quanh đường thẳng \(MN\) với \(M\) là trung điểm \(AD\) , \(N\) là trung điểm \(BC\) ta được một hình cầu tâm \(O\) bán kính $R = \dfrac{5}{2}$

Diện tích mặt cầu là \(S = 4\pi {R^2} = 4.\pi {\left( {\dfrac{5}{2}} \right)^2} = 25\pi \) \(\left( {cm} \right)\) .