Câu hỏi:
2 năm trước
Cho một tam giác đều $ABC$ có cạnh $AB = 8cm$, đường cao $AH$. Khi đó thể tích hình cầu được tạo thành khi quay nửa đường tròn nội tiếp tam giác $ABC$ một vòng quanh $AH$.
Trả lời bởi giáo viên
Đáp án đúng: c
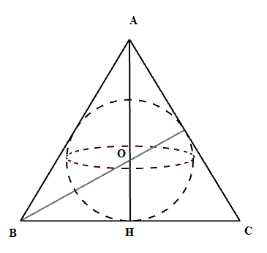
Vì \(\Delta ABC\) là tam giác đều nên tâm đường tròn nội tiếp trùng với trọng tâm \(O\) của tam giác.
Khi đó bán kính đường tròn nội tiếp là \(R = OH = \dfrac{{AH}}{3}\)
Xét tam giác vuông \(ABH\) có \(A{H^2} = A{B^2} - B{H^2} = {a^2} - {\left( {\dfrac{a}{2}} \right)^2} = \dfrac{{3{a^2}}}{4} \Rightarrow AH = \dfrac{{a\sqrt 3 }}{2}\)
Suy ra \(R = \dfrac{{a\sqrt 3 }}{6}\)
Khi quay nửa đường tròn nội tiếp tam giác $ABC$ một vòng quanh $AH$ ta được hình cầu bán kính \(R = \dfrac{{a\sqrt 3 }}{6}\)\( \Rightarrow V = \dfrac{4}{3}\pi {R^3} = \dfrac{4}{3}\pi .{\left( {\dfrac{{a\sqrt 3 }}{6}} \right)^3} = \dfrac{{\sqrt 3 \pi {a^3}}}{{54}}\)
Hướng dẫn giải:
Công thức thể tích hình cầu $V = \dfrac{4}{3}\pi {R^3}$
