Chọn câu sai. Cho hình trụ có bán kính đáy là R và chiều cao h . Khi đó
Ta có hình trụ có bán kính đáy là R và chiều cao h . Khi đó
+ Diện tích xung quanh của hình trụ là Sxq=2πRh nên A đúng
+ Diện tích toàn phần của hình trụ là Stp=2πRh+2πR2 nên B đúng
+ Thể tích khối trụ là V=πR2h nên C đúng, D sai.
Chọn câu sai.
Ta có
+ Thể tích hình nón có chiều cao h và bán kính đáy R là V=13πR2h nên A đúng
+ Diện tích hình cầu có bán kính R là S=4πR2 nên C đúng
+ Đường sinh của hình nón có chiều cao h và bán kính đáy R là l=√R2+h2 nên D đúng
+ Thể tích khối cầu có bán kính R là V=43πR3 nên B sai.
Tính diện tích xung quanh của một hình trụ có bán kính đáy là 4cm và chiều cao là 6cm .
Diện tích xung quanh của hình trụ là Sxq=2π.4.6=48π(cm2).
Diện tích toàn phần của một hình trụ có chu vi đường tròn đáy là 12cm và chiều cao là 4cm là
Gọi R là bán kính đường tròn đáy ta có 12=2πR⇒R=6π(cm)
Diện tích toàn phần của hình trụ là Stp=2π.6π.4+2π.(6π)2 =48+72π(cm2)
Một hình trụ có bán kính đáy bằng 5cm và diện tích xung quanh bằng 300π(cm2) . Chiều cao của hình trụ là
Gọi chiều cao của hình trụ là h. Ta có Sxq=2πR.h⇔2π.5.h=300π⇔h=30cm.
Một hình trụ có diện tích toàn phần gấp đôi diện tích xung quanh. Tính chiều cao hình trụ biết bán kính hình trụ là 1cm.
Gọi chiều cao của hình trụ là h.
Ta có Sxq=2πRh ; Stp=2πRh+2πR2 mà theo giả thiết thì Stp=2Sxq nên ta có
2πRh+2πR2=2.2πRh⇔2πR2=2πRh⇒h=R=1cm.
Một hình trụ có chiều cao bằng đường kính đáy. Biết thể tích của nó là 54π(cm3). Tính diện tích toàn phần của hình trụ.
Gọi hình trụ có bán kính đáy R và chiều cao h , từ đề bài suy ra h=2R .
Khi đó V=πR2h⇔π.R2.2R=54π⇒R3=27⇒R=3cm nên h=2R=6cm.
Diện tích toàn phần của hình trụ là Stp=2π.Rh+2πR2=2π.3.6+2π.32=54π(cm2)
Một hình nón có bán kính đáy bằng 5cm , chiều cao bằng 12cm.Tính diện tích xung quanh của hình nón.
Đường sinh của hình nón là l=√R2+h2=√52+122=13.
Diện tích xung quanh hình nón là Sxq=πRl=π.5.13=65π(cm2)
Tính thể tích của một hình nón cụt có các bán kính đáy bằng 4cm và 7cm, chiều cao bằng 11cm.
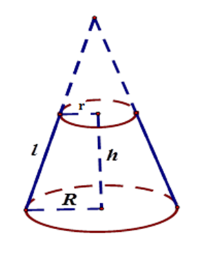
Thể tích nón cụt là V=13πh(R2+Rr+r2)=13.π.11(42+4.7+72)=341π(cm3)
Cho hai hình trụ. Hình trụ thứ nhất có bán kính đáy bằng nửa bán kính đáy của hình trụ thứ hai và có chiều cao gấp bốn lần chiều cao của hình trụ thứ hai. Tỉ số các thể tích của hình trụ thứ nhất và hình trụ thứ hai bằng:
Giả sử hình trụ thứ nhất có bán kính đáy là R và chiều cao là h. Thể tích hình trụ thứ nhất là: V1=πR2h (1)
Vì hình trụ thứ nhất có bán kính đáy bằng nửa bán kính đáy của hình trụ thứ hai và có chiều cao gấp bốn lần chiều cao của hình trụ thứ hai nên hình trụ thứ hai có bán kính đáy là 2R và chiều cao là h4.
Thể tích hình trụ thứ hai là: V2=π(2R)2.h4=πR2h (2)
Từ (1) và (2) suy ra V1=V2⇒V1V2=1
Một hình nón có diện tích xung quanh bằng 960cm2 , chu vi đáy bằng 48(cm). Đường sinh của hình nón đó bằng
Gọi R là bán kính đáy và l là đường sinh của hình nón.
Vì chu vi đáy là 48(cm)⇒2πR=48⇒R=24πcm.
Diện tích xung quanh Sxq=πRl⇔π.24π.l=960⇒l=40cm
Một hình nón có bán kính đáy bằng r và diện tích xung quanh gấp đôi diện tích đáy. Tính thể tích của hình nón theo r.
Gọi l là đường sinh của hình nón, h là chiều cao của hình nón.
Ta có diện tích xung quanh hình nón là Sxq=πRl, diện tích đáy là S=πr2
Vì diện tích xung quanh gấp đôi diện tích đáy nên πrl=2πr2⇒l=2r
Vì r2+h2=l2⇒h=√l2−r2=√(2r)2−r2=r√3
Khi đó thể tích khối nón là V=13πr2h=13πr2.√3r=√33πr3
Một hình nón và một hình trụ có bán kính đáy bằng nhau và chiều cao bằng nhau. Tỉ số các thể tích của hình trụ và hình nón bằng
Vì hình nón và một hình trụ có bán kính đáy bằng nhau và chiều cao bằng nhau nên gọi h là chiều cao và R là bán kính đáy khi đó thể tích hình nón Vn=13πR2h và thể tích hình trụ Vt=πR2h
Tỉ số thể tích của hình trụ và hình nón là VtVn=πR2h13πR2h=3.
Tính bán kính của một hình cầu biết thể tích của hình cầu bằng 123(cm3) (làm tròn đến số thập phân thứ nhất). Lấy π=3,14.
Gọi bán kính mặt cầu là R thì thể tích khối cầu là V=43πR3⇔43.3,14.R3=123⇔R≈3,1cm
Chiều cao của một hình trụ gấp rưỡi bán kính đáy của nó. Tỉ số thể tích của hình trụ này và thể tích hình cầu có bán kính bằng bán kính đáy của hình trụ là:
Giả sử hình trụ có bán kính đáy R.
Suy ra chiều cao của nó là 1,5R.
Thể tích hình trụ là V1=πR2h=πR2.1,5R=1,5πR3
Thể tích hình cầu có bán kính R là V2=43πR3
V1V2=1,5πR343πR3=98.
Một hình cầu được đặt khít bên trong một hình trụ, biết đường kính hình cầu là 20cm.
Tính thể tích hình trụ.
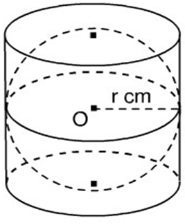
Bán kính hình cầu là r=20:2=10cm
Vì hình cầu nội tiếp hình trụ nên bán kính hình cầu bằng bán kính đáy hình trụ và đường kính hình cầu bằng chiều cao hình trụ.
Do đó hình trụ có bán kính đáy là r=10cm và chiều cao là h=2r=20cm
Thể tích hình trụ là V=πr2h=π.102.20=2000π(cm3)
Cho một hình trụ, một hình nón và một hình cầu có thể tích bằng nhau. Bán kính đáy của hình trụ, bán kính đáy của hình nón và bán kính của hình cầu đều bằng R. Tính các chiều cao h1 của hình trụ và h2 của hình nón theo R.
+ Thể tích hình trụ : V1=πR2h1.
+ Thể tích hình nón : V2=13πR2h2.
+ Thể tích hình cầu : V3=43πR3
Ta có V1=V2=V3
Nên {πR2h1=43πR313πR2h2=43πR3 ⇔{h1=43Rh2=4R
Một hình nón có bán kính đáy bằng 2cm, chiều cao bằng đường kính một hình cầu. Diện tích toàn phần hình nón bằng diện tích mặt cầu. Tính chiều cao hình nón.
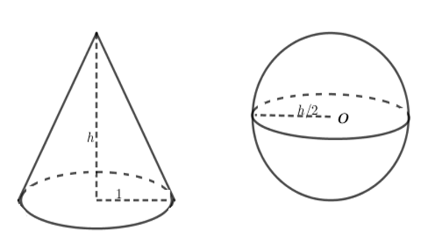
Gọi h là chiều cao hình nón (h>0) . Đường sinh của hình nón bằng l=√h2+4
Diện tích toàn phần của hình nón Stp=π.2.√h2+4+π.22=π(2√h2+4+4)(cm2)
Vì chiều cao hình nón bằng đường kính hình cầu nên bán kính hình cầu là h2(cm)
Diện tích mặt cầu là S=4π.(h2)2=πh2
Theo bài ra ta có
π(2√h2+4+4)=πh2
⇔2√h2+4+4=h2⇔2√h2+4=h2−4(h>2)
⇒4(h2+4)=h4−8h2+16⇔h4−12h2=0
⇔[h2=0h2=12⇔[h=0(L)h=−2√3(L)h=2√3(N)
Vậy chiều cao hình nón là 2√3cm.

