Khi đó tam giác CMN là tam giác
Theo chứng minh ở câu 14 ta có ΔACN=ΔBCM.Do đóCN=CM.
Vì vậy ΔCMN là tam giác cân tại C(1).
Lại có ^CMA=12sdAC=12.900=450⇒^CMN=450.
ΔCMN là tam giác cân tại Cnên ^CNM=^CMN=450. Tổng ba góc trong một tam giác bằng 1800. Nên ^CMN+^CNM+^MCN=1800⇒450+450+^MCN=1800.
Do đó ^MCN=900(2).
Từ (1) và (2) suy ra ΔCMN vuông cân tại C .
Chọn câu đúng.
Xét ΔACN và ΔBCM có:
+ AC=BC (vì C là điểm chính giữa của cung AB)
+ ^CAN=^CBN (hai góc nội tiếp cùng chắn cung CM)
+ Theo giả thiết ta có AN=BM.
Do đó ΔACN=ΔBCM(c.g.c). Hai tam giác bằng nhau nên diện tích bằng nhau. Do đó S1=S2.
Chọn câu đúng.
Xét ΔACN và ΔBCM có:
+ AC=BC (vì C là điểm chính giữa của cung AB)
+ ^CAN=^CBN (hai góc nội tiếp cùng chắn cung CM)
+ Theo giả thiết ta có AN=BM.
Do đó ΔACN=ΔBCM(c.g.c). Hai tam giác bằng nhau nên diện tích bằng nhau. Do đó S1=S2.
Chọn câu đúng.
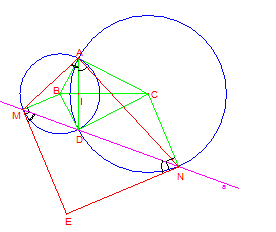
Trong ΔAMN có: ^MAN+^AMN+^ANM=180o, mà: ^MEN+^MAN=180o (theo câu trước)
suy ra: ^MEN=^AMN+^ANM
Ta lại có: ^AND=^ACB=12^ACD,^AMD=^ABC=12^ABD (góc ở tâm và góc nội tiếp cùng chắn một cung)
Mà: DABC vuông tại A nên: ^MEN=90o (không đổi)
Chọn câu đúng
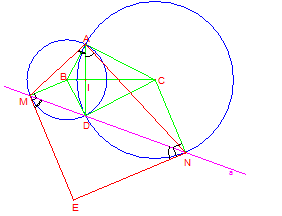
Ta có:
^DME=^DAM ( góc tạo bởi tia tuyến và dây cung)
^DNE=^DAN (góc tạo bởi tia tuyến và dây cung)
Suy ra: ^DME+^DNE=^DAM+^DAN
Trong DMNE có: ^MEN+^EMN+^ENM=180o ,
suy ra: ^MEN+^DAM+^DAN=180o
Hay: ^MEN+^MAN=180o.
Chọn câu đúng

Ta có:
^DME=^DAM ( góc tạo bởi tia tuyến và dây cung)
^DNE=^DAN (góc tạo bởi tia tuyến và dây cung)
Suy ra: ^DME+^DNE=^DAM+^DAN
Trong DMNE có: ^MEN+^EMN+^ENM=180o ,
suy ra: ^MEN+^DAM+^DAN=180o
Hay: ^MEN+^MAN=180o.
Chọn khẳng định đúng:
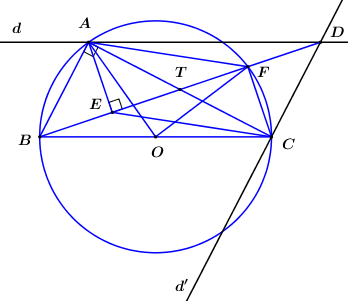
Do tứ giác AECD nội tiếp (cmt) nên: ∠CAE=∠CDE (hai góc nội tiếp cùng chắn cung CE)
Mà ∠CDE=∠ABF (so le trong)
⇒∠CAE=∠ABF.
Mặt khác: ∠AOF=2∠ABF (góc ở tâm và góc nội tiếp cùng chắn cung AF)
⇒∠AOF=2∠CAE.
Tứ giác AECD nội tiếp đường tròn nào dưới đây:
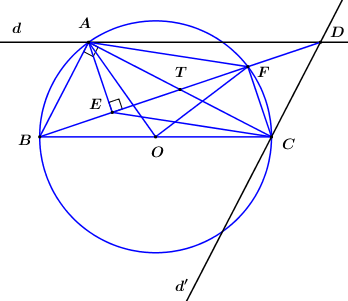
Vì ΔABC vuông tại A và nội tiếp (O) nên BC là đường kính của (O).
Ta có: {AB⊥ACCD//AB(gt)⇒AC⊥CD (từ vuông góc đến song song) ⇒∠ACD=900.
Xét tứ giác AECD có: ∠AED=∠ACD=900 ⇒AECD là tứ giác nội tiếp đường tròn đường kính AD. (Tứ giác có 2 đỉnh kề cùng nhìn một cạnh dưới các góc bằng nhau).
Tứ giác AECF là hình gì?
Do tứ giác AECD là tứ giác nội tiếp (cmt) nên: ∠ACE=∠ADE (2 góc nội tiếp cùng chắn cung AE).
Ta có: ∠ADE=∠DBC (so le trong do AD//BC) ⇒∠ACE=∠DBC.
Mà ∠DBC=∠FBC=∠FAC (hai góc nội tiếp cùng chắn cung FC)
⇒∠ACE=∠FAC. Mà hai góc này ở vị trí so le trong nên AF//EC (dhnb) (1)
Mặt khác: ∠CFE=900 (góc nội tiếp chắn nửa đường tròn) nên CF⊥FE hay CF⊥BD.
Mà AE⊥BD(gt) nên AE//CF (từ vuông góc đến song song) (2)
Từ (1) và (2) suy ra tứ giác AECF là hình bình hành (tứ giác có các cặp cạnh đối song song).
Chọn khẳng định đúng về tích DF.BD?
Gọi {T}=AC∩BD.
Ta có: {AB//CDAD//BC(gt)⇒ABCD là hình bình hành (dhnb) ⇒TA=TC,TB=TD và AB=CD (tính chất).
Xét ΔDCT vuông tại C có CF⊥BD(cmt)⇒CF⊥DT ⇒CF là đường cao nên:
CD2=DF.DT (hệ thức lượng trong tam giác vuông)
⇒2.CD2=2.DF.DT=(2.DT).DF=DB.DF.
Mà AB=CD (cmt).
Vậy DF.DB=2AB2.
Chọn khẳng định đúng về hai đường thẳng nối tâm hai đường tròn ngoại tiếp hai tam giác MBE,MCD
Ta có ∠ABC=∠AGE(cmt) nên EBMG là tứ giác nội tiếp (tứ giác có góc ngoài bằng góc trong tại đỉnh đối diện).
⇒ Đường nối tâm hai đường tròn ngoại tiếp hai tam giác MBE,MCD là đường nối tâm hai đường tròn ngoại tiếp hai tứ giác GDCM và EBMG.
Giao của hai tứ giác GDCM và EBMG là GM.
⇒ Đường nối tâm vuông góc với GM(∗)
Gọi {F}=AH∩BC ⇒AF⊥BC⇒∠AFB=900.
Mà ∠BDA=900 ⇒ADFB nội tiếp (tứ giác có 2 đỉnh kề cùng nhìn một cạnh dưới các góc bằng nhau).
⇒∠BAC=∠DFM (1) (góc ngoài và góc trong tại đỉnh đối diện của tứ giác nội tiếp).
Mà ∠EDH=∠EAH(2) (Hai góc nội tiếp cùng chắn cung EH).
∠HDM=∠HBM=∠DBM (DM là trung tuyến của ΔBDC vuông tại D nên DM=12BC=BM).
∠DBM=∠HAD (Cùng phụ ∠ACB)
⇒∠HDM=∠HAD(3)
Từ (1), (2) và (3) suy ra
∠EDM=∠EDH+∠HDM=∠EAH+∠HAD=∠BAC=∠DFM=∠KDM
Xét ΔFDM và ΔDKM có: ∠KMD chung; ∠DFM=∠KDM (cmt)
⇒ΔFDM∼ΔDKM(g.g) ⇒MDKM=FMMD⇒MD2=FM.KM
Có: ΔGCM∼ΔCAM(cmt)⇒MCAM=GMMC⇒MC2=MG.MA
Mà MD=MC(cmt) ⇒FM.KM=MG.MA⇒FMGM=MAMK
⇒ΔFGM∼ΔAKM(c.g.c)⇒∠FGM=∠AKM (2 góc tương ứng)
⇒AGFK là tứ giác nội tiếp (tứ giác có góc ngoài bằng góc trong tại đỉnh đối diện).
⇒∠AFK=∠AGK=900 (2 góc nội tiếp cùng chắn cung AK) ⇒KG⊥AG hay KG⊥GM (**)
Từ (*) và (**) suy ra đường nối tâm hai đường tròn ngoại tiếp hai tam giác MBE,MCD song song với KG.
Hai đường thẳng DE và BC cắt nhau tại K. Chọn khẳng định đúng?
Ta có ∠AGD=∠AED (2 góc nội tiếp cùng chắn cung AD)
Mà ∠AED=∠ACB (góc ngoài và góc trong tại đỉnh đối diện của tứ giác nội tiếp BEDC)
⇒∠AGD=∠ACB=∠DCM.
Lại có ∠AGD+∠DGM=1800 (kề bù) ⇒∠DGM+∠DCM=1800.
⇒GDCM là tứ giác nội tiếp (dhnb) ⇒∠MGC=∠MDC (hai góc nội tiếp cùng chắn cung MC).
Lại có DM=12BC=MC (định lí đường trung tuyến trong tam giác vuông) ⇒ΔMCD cân tại M.
⇒∠MDC=∠MCD (2 góc ở đáy của tam giác cân).
⇒∠MGC=∠MCD=∠MCA.
Xét ΔGCM và ΔCAM có: ∠AMC chung ; ∠MAC=∠GCM (cmt)
⇒ΔGCM∼ΔCAM(g.g) ⇒∠MAC=∠GCM (2 góc tương ứng)
Gọi M là trung điểm của BC. Đường tròn đường kính AH cắt AM tại điểm G (G khác A). Chứng Chọn khẳng định đúng?
Ta có: ∠AEH=∠ADH=900⇒∠AEH+∠ADH=1800
⇒AEHD nội tiếp đường tròn đường kính AH (định nghĩa)
Mà đường tròn đường kính AH cắt AM tại G.
⇒ Năm điểm A,E,H,G,D cùng thuộc một đường tròn.
⇒∠AGE=∠ADE (2 góc nội tiếp cùng chắn cung AE)
Mà ∠ABC=∠ADE (góc ngoài và góc trong tại đỉnh đối diện của tứ giác nội tiếp BEDC)
⇒∠ABC=∠AGE.
Xét ΔABM và ΔAGE có: ∠ABC=∠AGE (cmt); ∠BAM chung.
⇒ΔABM∼ΔAGE(g.g)⇒AEAM=AGAB (2 cặp cạnh tương ứng tỉ lệ)
⇒AE.AB=AG.AM
Tứ giác BEDC nội tiếp đường tròn nào dưới đây:
Ta có: BD,CE là các đường cao của ΔABC nên {BD⊥ACCE⊥AB⇒∠BDC=∠BEC=900
⇒BEDC là tứ giác nội tiếp đường tròn đường kính BC (Tứ giác có hai đỉnh kề một cạnh cùng nhìn cạnh đối diện các góc bằng nhau).
Đường tròn ngoại tiếp ΔAKD luôn đi qua một điểm cố định khác A khi điểm D di động trên cung nhỏ AC?
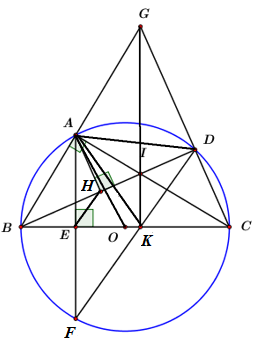
Ta có: OA=12BC=OB (đường trung tuyến ứng với cạnh huyền trong tam giác vuông)
⇒ΔOAB cân tại O ⇒∠OAB=∠OBA=∠ABC=12sdcungAC (3)
Lại có: ∠CKD=12(sdcungCD+sdcngBF)=12(sdcungCD+sdcungAB)
Vì OH⊥BD(gt)⇒cungAB=cungAD
⇒∠CKD=12(sdcungCD+sdcungAD)=12sdcungAC(4)
Từ (3) và (4) ⇒∠OAB=∠CKD
⇒OKDA là tứ giác nội tiếp. (tứ giác có góc ngoài bằng góc trong tại đỉnh đối diện)
⇒ Đường tròn ngoại tiếp ΔAKD đi qua điểm O cố định.
Chọn khẳng định đúng:
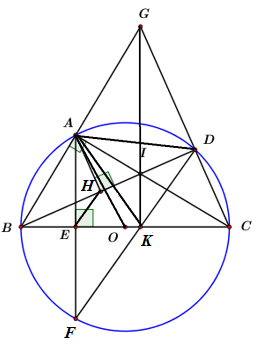
Xét ΔBHE và ΔBCI có:
Ta có: BC⊥AF⇒cungAB=cungFB (đường kính vuông góc với một dây thì đi qua điểm ở chính giữa của cung căng dây đó).
⇒∠BDF=∠BCA (hai góc nội tiếp chắn 2 cung bằng nhau).
Hay ∠IDK=∠ICK
⇒CDJK là tức giác nội tiếp. (tứ giác có 2 đỉnh kề nhau cùng nhìn 1 cạnh dưới các góc bằng nhau)
⇒∠IKC+∠IDC=1800. Mà ∠IDC=∠BDC=900(cmt)
⇒∠IKC=900⇒IK⊥BC(1)
Xét ΔGBC có {AC⊥BGBD⊥CGAC∩BD={I}
⇒I là trực tâm ΔGBC ⇒GI⊥BC(2)
Từ (1) và (2) ⇒G,I,K thằng hàng.
Chọn khẳng định đúng:
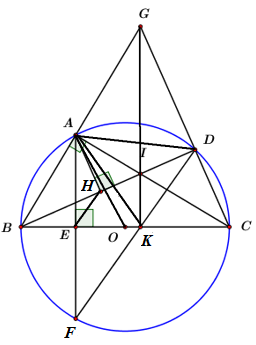
Xét tứ giác ABEH ta có: ∠AEB=∠AHB=900(gt)
\Rightarrow ABEH là tứ giác nội tiếp. (tứ giác có hai đỉnh kề nhau cùng nhìn cạnh đối diện dưới các góc bằng nhau)
\Rightarrow \angle BHE = \angle BAE (hai góc nội tiếp cùng chắn cung BE)
Mà \angle BAE = \angle BCA (hai góc cùng phụ \angle ABC)
\Rightarrow \angle BHE = \angle BCA = \angle BCI
Xét \Delta BHE và \Delta BCI có:
\angle IBC\, chung
\angle BHE = \angle BCI\,\,\left( {cmt} \right)
\Rightarrow \dfrac{{BE}}{{BI}} = \dfrac{{BH}}{{BC}} \Rightarrow BE.BC = BH.BI\,
Tứ giác AIDG nội tiếp đường tròn nào sau đây?
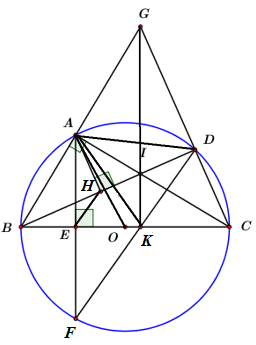
Ta có: \angle BAC,\angle BDC là góc nội tiếp chắn nửa đường tròn \left( O \right) \Rightarrow \angle BAC = \angle BDC = {90^0}.
\Rightarrow \angle GAI = \angle GDI = {90^0}
Xét tứ giác AIDG ta có: \angle GAI + \angle GDI = {90^0} + {90^0} = {180^0}
Suy ra AIDG là tứ giác nội tiếp đường tròn đường kính GI.
Chọn câu đúng.
Xét \Delta ACN và \Delta BCM có:
+ AC = BC (vì C là điểm chính giữa của cung AB)
+ \widehat {CAN} = \widehat {CBN} (hai góc nội tiếp cùng chắn cung CM)
+ Theo giả thiết ta có AN = BM.
Do đó \Delta ACN = \Delta BCM\,\,\left( {c.g.c} \right). Hai tam giác bằng nhau nên diện tích bằng nhau. Do đó {S_1} = {S_2}.
Chọn câu đúng

Ta có:
\widehat {DME} = \widehat {DAM} ( góc tạo bởi tia tuyến và dây cung)
\widehat {DNE} = \widehat {DAN} (góc tạo bởi tia tuyến và dây cung)
Suy ra: \widehat {DME} + \widehat {DNE} = \widehat {DAM} + \widehat {DAN}
Trong DMNE có: \widehat {MEN} + \widehat {EMN} + \widehat {ENM} = {180^o} ,
suy ra: \widehat {MEN} + \widehat {DAM} + \widehat {DAN} = {180^o}
Hay: \widehat {MEN} + \widehat {MAN} = {180^o}.

