Câu hỏi:
2 năm trước
Cho tam giác $ABC$ vuông cân tại $A$ có cạnh góc vuông bằng $a$. Tính diện tích mặt cầu được tạo thành khi quay nửa đường tròn ngoại tiếp tam giác $ABC$ một vòng quanh cạnh $BC$.
Trả lời bởi giáo viên
Đáp án đúng: a
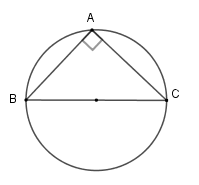
Vì tam giác \(ABC\) vuông tại \(A\) nên có đường tròn ngoại tiếp là đường tròn đường kính \(BC\) .
Bán kính đường tròn ngoại tiếp tam giác là \(R = \dfrac{{BC}}{2}\)
Theo định lý Pytago ta có \(B{C^2} = A{B^2} + A{C^2} = 2{a^2} \Rightarrow BC = a\sqrt 2 \) \( \Rightarrow R = \dfrac{{a\sqrt 2 }}{2}\)
Khi quay nửa đường tròn ngoại tiếp tam giác $ABC$ một vòng quanh cạnh $BC$ ta được hình cầu có bán kính \(R = \dfrac{{a\sqrt 2 }}{2}\) nên diện tích mặt cầu là \(S = 4\pi {R^2} = 4\pi {\left( {\dfrac{{a\sqrt 2 }}{2}} \right)^2} = 2\pi {a^2}\) .
Hướng dẫn giải:
Xác định tâm và bán kính đường tròn ngoại tiếp tam giác \(ABC\)
Sử dụng công thức diện tích mặt cầu $S = 4\pi {R^2}$
