Cho hình bình hành $ABCD$ , hai đường chéo cắt nhau tại $I$ . Từ $A$ kẻ các đường vuông góc với $BC$ , $CD$ , $DB$ thứ tự tại $H,E,K$ . Xét các khẳng định sau:
I. Bốn điểm $A,H,C,E$ nằm trên một đường tròn.
II. Bốn điểm $A,K,D,E$ nằm trên một đường tròn.
III. Bốn điểm $A,H,K,B$ nằm trên một đường tròn.
IV. Bốn điểm $K,I,E,H$ nằm trên một đường tròn.
Chọn khẳng định đúng.
Trả lời bởi giáo viên
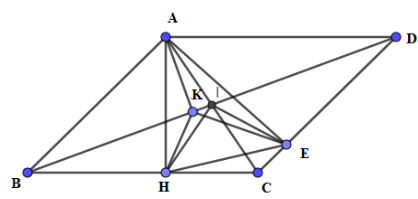
\(AH \bot BC,AE \bot CD \Rightarrow \) bốn điểm $A,H,C,E$ nằm trên đường tròn đường kính$AC$ , $I$ là trung điểm của $AC$
\( \Rightarrow \) $I$ là tâm đường tròn đường kính $AC$
$ \Rightarrow \widehat {HIE} = 2\widehat {HAE} = 2\left( {\widehat {HAC} + \widehat {EAC}} \right)$ \( = 2\left( {{{90}^0} - \widehat {ACB} + {{90}^0} - \widehat {ACE}} \right) = 2\left( {{{180}^0} - \widehat {BCD}} \right)\)
Lại có \(AH \bot BC,AK \bot BD,AE \bot CD\) nên bốn đỉnh \(A,K,E,D\) nằm trên đường tròn đường kính \(AD\) và bốn đỉnh \(A;K;H;B\) nằm trên đường tròn đường kính \(AB\) \( \Rightarrow \widehat {EKD} = \widehat {EAD}\) và \(\widehat {BKH} = \widehat {BAH}\)
\( \Rightarrow \widehat {HKE} = {180^0} - \widehat {EKD} - \widehat {BKH} = {180^0} - \widehat {EAD} - \widehat {BAH}\\ = {90^0} - \widehat {EAD} + {90^0} - \widehat {BAH} = \widehat {ADC} + \widehat {ABC} = 2\left( {{{180}^0} - \widehat {BCD}} \right)\)
Suy ra $K$ và $I$ cùng nhìn đoạn $HE$ dưới một góc \(2\left( {{{180}^0} - \widehat {BCD}} \right)\)
Vậy $K,I,E,H$ nằm trên một đường tròn.