Cho tam giác $ABC$ cân tại $A,M$ là điểm trên cạnh đáy $BC$. Qua $M$ kẻ các đường thẳng song song với hai cạnh bên cắt hai cạnh đó tại $D$ và $E$. Gọi $N$ là điểm đối xứng của $M$ qua $DE$. Quỹ tích các điểm $N$ là:
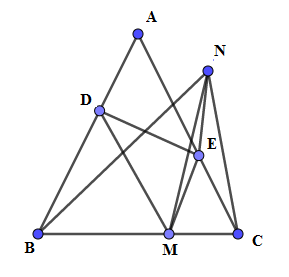
Ta có $MD{\rm{//}}AC,ME{\rm{//}}AB$
\( \Rightarrow \widehat {BDM} = \hat A = \widehat {MEC} \)
\(\Rightarrow DB = DM,\;EC = EM.\)
$M,N$ đối xứng nhau qua $DE$
\( \Rightarrow DN = DM;\;\;EM = EN.\)
\( \Rightarrow \) $D$ là tâm đường tròn ngoại tiếp tam giác $BMN$
\( \Rightarrow \widehat {BNM} = \dfrac{1}{2}\widehat {BDM} = \dfrac{1}{2}\widehat A\) (góc nội tiếp bằng nửa góc ở tâm cùng chắn cung $BM$ ).
Tương tự, $E$ là tâm đường tròn ngoại tiếp tam giác $CMN$ .
\( \Rightarrow \widehat {MNC} = \dfrac{1}{2}\widehat {MEC} = \dfrac{1}{2}\widehat A\) \( \Rightarrow \widehat {BNC} = \widehat {BNM} + \widehat {MNC} = \widehat A\)
Suy ra $N$ nhìn đoạn $BC$ dưới một góc bằng \(\widehat {BAC}\) không đổi.
Nên quỹ tích các điểm $N$ là cung chứa góc bằng \(\widehat {BAC}\) dựng trên đoạn $BC$ .
Cho đoạn thẳng \(AB = 10cm\), \(M\) là trung điểm của \(AB\). Quỹ tích các điểm \(C\) trong mặt phẳng thỏa mãn tam giác \(ABC\) có \(C{A^2} + C{B^2} = 100\) là:
Vì \(C{A^2} + C{B^2} = 100 = A{B^2}\) nên \(\Delta ABC\) là tam giác vuông tại \(C\) hay điểm \(C\) luôn nhìn đoạn \(AB\) một góc \({90^0}\).
Do đó quỹ tích các điểm \(C\) là đường tròn đường kính \(AB = 10cm\) hay đường tròn tâm \(M\) bán kính \(5cm\).
Cho tam giác ABC nội tiếp đường tròn (O,R), gọi H là trực tâm, I và O là tâm đường tròn nội tiếp và ngoại tiếp tam giác ABC, đồng thời AH bằng bán kính đường tròn ngoại tiếp tam giác ABC. Ta có các nhận xét sau:
(I): O nằm trên cung tròn nhìn về một phía của BC dưới góc \({120^\circ }\).
(II): I nằm trên cung tròn nhìn về một phía của BC dưới góc \({120^\circ }\).
(III): H trên cung tròn nhìn về một phía của BC dưới góc \({120^\circ }\).
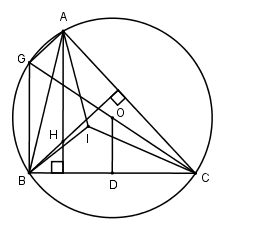
Gọi D là trung điểm của BC. Suy ra \(OD \bot BC\).
Kéo dài OC cắt đường tròn tại điểm G ta có : \(\widehat {CBG} = {90^0} \Rightarrow BG \bot BC \Rightarrow BG//AH\)
\( \Rightarrow OD = \dfrac{1}{2}BG\) (tính chất đường trung bình).
Ta có: \(\widehat {CAG} = {90^0} \Rightarrow AG \bot AC \Leftrightarrow AG//BH \Rightarrow \) AHBG là hình bình hành \( \Rightarrow BG = AH \Rightarrow AH = 2OD\)
Theo giả thiết $AH = R \Rightarrow R = OB = 2OD$
Tam giác OBD là tam giác vuông có $OB = 2OD \Rightarrow \widehat {OBD} = {30^0}$
$ \Rightarrow \widehat {BOC} = {120^0} \Rightarrow \widehat {BAC} = {60^0}$
H là trực tâm của tam giác ABC\( \Rightarrow CH \bot AB,BH \bot AC \Rightarrow \widehat {BHC} = {120^\circ }.\)
\(\widehat {BIC} = {180^0} - \dfrac{1}{2}\left( {\widehat {ABC} + \widehat {ACB}} \right)\)\( = {180^0} - \dfrac{1}{2}\left( {{{180}^0} - \widehat {BAC}} \right) = {90^0} + \dfrac{1}{2}\widehat {BAC} = {120^0}\)
Ta thấy \(\widehat {BOC} = \widehat {BHC} = \widehat {BIC} = {120^\circ }\)nên ba điểm O, H, I nằm trên cung tròn nhìn về một phía của BC dưới góc \({120^0}\).
Cho nửa đường tròn đường kính AB, dây MN có độ dài bằng bán kính R của đường tròn, M thuộc cung AN. Các tia AM và BN cắt nhau ở I, dây AN và BM cắt nhau ở K. Với vị trí nào của dây MN thì diện tích tam giác IAB lớn nhất? Tính diện tích đó theo bán kính R.
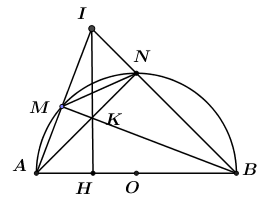
Gọi H là chân đường cao kẻ từ I đến cạnh AB.
Khi đó ta có: \({S_{IAB}} = \dfrac{1}{2}IH.AB.\)
Ta có AB là đường kính \( \Rightarrow {S_{IAB}}\;\;Max \Leftrightarrow IH\;Max \Leftrightarrow \) H trùng với O.
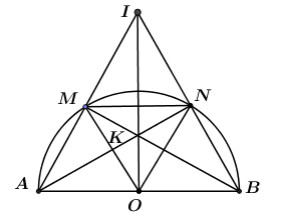
Khi H trùng với O thì OI vừa là đường cao vừa là đường trung tuyến của tam giác \( \Rightarrow \Delta IAB\) cân tại I.
Lại có \(\dfrac{{MN}}{{AB}} = \dfrac{R}{{2R}} = \dfrac{1}{2} \Rightarrow MN\) là đường trung bình của tam giác \(\Delta ABC\).
\( \Rightarrow MN//BC.\)
Xét \(\Delta MON\) có \(MO = ON = MN = R \Rightarrow \Delta MON\) là tam giác đều.
Tam giác IAB cân tại I có MN là đường trung bình \( \Rightarrow \) M và N lần lượt là trung điểm của AM và AB.
Lại có O là trung điểm của AB \( \Rightarrow OM;\;\;ON\) cũng là hai đường trung bình của tam giác IAB.
\( \Rightarrow \left\{ \begin{array}{l}ON//IM\\OM//IN\end{array} \right. \Rightarrow \) tứ giác IMON là hình bình hành.
Lại có hai đường chéo OI và MN vuông góc với nhau \(\left( {do\;MN//AB;\;\;OI \bot AB} \right).\)
\( \Rightarrow IMON\) là hình thoi \( \Rightarrow MI = IN = OM = R \Rightarrow IA = 2IM = 2R.\)
Xét tam giác AOI vuông tại O ta có: \(OI = \sqrt {I{A^2} - O{A^2}} = \sqrt {4{R^2} - {R^2}} = R\sqrt 3 .\)
\( \Rightarrow {S_{IAB}} = \dfrac{1}{2}OI.AB = \dfrac{1}{2}.R\sqrt 3 .2R = {R^2}\sqrt 3 .\)

