Câu hỏi:
2 năm trước
Cho tam giác ABC nội tiếp đường tròn (O,R), gọi H là trực tâm, I và O là tâm đường tròn nội tiếp và ngoại tiếp tam giác ABC, đồng thời AH bằng bán kính đường tròn ngoại tiếp tam giác ABC. Ta có các nhận xét sau:
(I): O nằm trên cung tròn nhìn về một phía của BC dưới góc \({120^\circ }\).
(II): I nằm trên cung tròn nhìn về một phía của BC dưới góc \({120^\circ }\).
(III): H trên cung tròn nhìn về một phía của BC dưới góc \({120^\circ }\).
Trả lời bởi giáo viên
Đáp án đúng: a
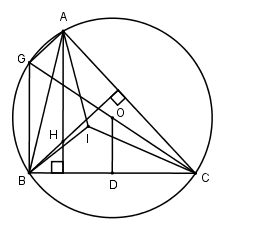
Gọi D là trung điểm của BC. Suy ra \(OD \bot BC\).
Kéo dài OC cắt đường tròn tại điểm G ta có : \(\widehat {CBG} = {90^0} \Rightarrow BG \bot BC \Rightarrow BG//AH\)
\( \Rightarrow OD = \dfrac{1}{2}BG\) (tính chất đường trung bình).
Ta có: \(\widehat {CAG} = {90^0} \Rightarrow AG \bot AC \Leftrightarrow AG//BH \Rightarrow \) AHBG là hình bình hành \( \Rightarrow BG = AH \Rightarrow AH = 2OD\)
Theo giả thiết $AH = R \Rightarrow R = OB = 2OD$
Tam giác OBD là tam giác vuông có $OB = 2OD \Rightarrow \widehat {OBD} = {30^0}$
$ \Rightarrow \widehat {BOC} = {120^0} \Rightarrow \widehat {BAC} = {60^0}$
H là trực tâm của tam giác ABC\( \Rightarrow CH \bot AB,BH \bot AC \Rightarrow \widehat {BHC} = {120^\circ }.\)
\(\widehat {BIC} = {180^0} - \dfrac{1}{2}\left( {\widehat {ABC} + \widehat {ACB}} \right)\)\( = {180^0} - \dfrac{1}{2}\left( {{{180}^0} - \widehat {BAC}} \right) = {90^0} + \dfrac{1}{2}\widehat {BAC} = {120^0}\)
Ta thấy \(\widehat {BOC} = \widehat {BHC} = \widehat {BIC} = {120^\circ }\)nên ba điểm O, H, I nằm trên cung tròn nhìn về một phía của BC dưới góc \({120^0}\).
Hướng dẫn giải:
Sử dụng tính chất đường trung bình, tính chất hình bình hành và quỹ tích cung chứa góc.
Hai điểm B, C cố định. Quỹ tích các điểm M thỏa mãn \(\widehat {BMC} = \alpha \) không đổi là 2 cung chứa góc \(\alpha \) dựng trên BC.
