Câu hỏi:
2 năm trước
Cho tam giác $ABC$ cân tại $A,M$ là điểm trên cạnh đáy $BC$. Qua $M$ kẻ các đường thẳng song song với hai cạnh bên cắt hai cạnh đó tại $D$ và $E$. Gọi $N$ là điểm đối xứng của $M$ qua $DE$. Quỹ tích các điểm $N$ là:
Trả lời bởi giáo viên
Đáp án đúng: a
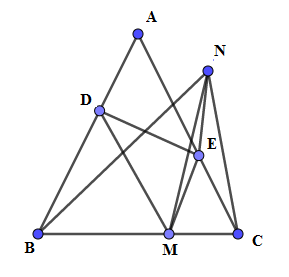
Ta có $MD{\rm{//}}AC,ME{\rm{//}}AB$
\( \Rightarrow \widehat {BDM} = \hat A = \widehat {MEC} \)
\(\Rightarrow DB = DM,\;EC = EM.\)
$M,N$ đối xứng nhau qua $DE$
\( \Rightarrow DN = DM;\;\;EM = EN.\)
\( \Rightarrow \) $D$ là tâm đường tròn ngoại tiếp tam giác $BMN$
\( \Rightarrow \widehat {BNM} = \dfrac{1}{2}\widehat {BDM} = \dfrac{1}{2}\widehat A\) (góc nội tiếp bằng nửa góc ở tâm cùng chắn cung $BM$ ).
Tương tự, $E$ là tâm đường tròn ngoại tiếp tam giác $CMN$ .
\( \Rightarrow \widehat {MNC} = \dfrac{1}{2}\widehat {MEC} = \dfrac{1}{2}\widehat A\) \( \Rightarrow \widehat {BNC} = \widehat {BNM} + \widehat {MNC} = \widehat A\)
Suy ra $N$ nhìn đoạn $BC$ dưới một góc bằng \(\widehat {BAC}\) không đổi.
Nên quỹ tích các điểm $N$ là cung chứa góc bằng \(\widehat {BAC}\) dựng trên đoạn $BC$ .
