Câu hỏi:
2 năm trước
Cho nửa đường tròn đường kính AB, dây MN có độ dài bằng bán kính R của đường tròn, M thuộc cung AN. Các tia AM và BN cắt nhau ở I, dây AN và BM cắt nhau ở K. Với vị trí nào của dây MN thì diện tích tam giác IAB lớn nhất? Tính diện tích đó theo bán kính R.
Trả lời bởi giáo viên
Đáp án đúng: d
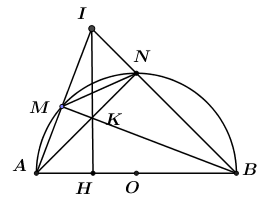
Gọi H là chân đường cao kẻ từ I đến cạnh AB.
Khi đó ta có: \({S_{IAB}} = \dfrac{1}{2}IH.AB.\)
Ta có AB là đường kính \( \Rightarrow {S_{IAB}}\;\;Max \Leftrightarrow IH\;Max \Leftrightarrow \) H trùng với O.
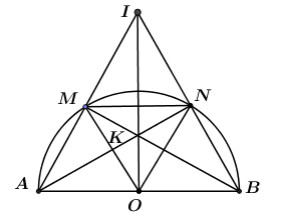
Khi H trùng với O thì OI vừa là đường cao vừa là đường trung tuyến của tam giác \( \Rightarrow \Delta IAB\) cân tại I.
Lại có \(\dfrac{{MN}}{{AB}} = \dfrac{R}{{2R}} = \dfrac{1}{2} \Rightarrow MN\) là đường trung bình của tam giác \(\Delta ABC\).
\( \Rightarrow MN//BC.\)
Xét \(\Delta MON\) có \(MO = ON = MN = R \Rightarrow \Delta MON\) là tam giác đều.
Tam giác IAB cân tại I có MN là đường trung bình \( \Rightarrow \) M và N lần lượt là trung điểm của AM và AB.
Lại có O là trung điểm của AB \( \Rightarrow OM;\;\;ON\) cũng là hai đường trung bình của tam giác IAB.
\( \Rightarrow \left\{ \begin{array}{l}ON//IM\\OM//IN\end{array} \right. \Rightarrow \) tứ giác IMON là hình bình hành.
Lại có hai đường chéo OI và MN vuông góc với nhau \(\left( {do\;MN//AB;\;\;OI \bot AB} \right).\)
\( \Rightarrow IMON\) là hình thoi \( \Rightarrow MI = IN = OM = R \Rightarrow IA = 2IM = 2R.\)
Xét tam giác AOI vuông tại O ta có: \(OI = \sqrt {I{A^2} - O{A^2}} = \sqrt {4{R^2} - {R^2}} = R\sqrt 3 .\)
\( \Rightarrow {S_{IAB}} = \dfrac{1}{2}OI.AB = \dfrac{1}{2}.R\sqrt 3 .2R = {R^2}\sqrt 3 .\)
Hướng dẫn giải:
Sử dụng tính chất hình bình hành, định lý Pytago và quỹ tích cung chứa góc
Hai điểm B, C cố định. Quỹ tích các điểm M thỏa mãn \(\widehat {BMC} = \alpha \) không đổi là 2 cung chứa góc \(\alpha \) dựng trên BC.
