Câu hỏi:
2 năm trước
Cho đường tròn đường kính $AB$ cố định, $M$ là một điểm chạy trên đường tròn. Trên tia đối của tia $MA$ lấy điểm $I$ sao cho $MI = 2MB$. Quỹ tích các điểm $I$ là:
Trả lời bởi giáo viên
Đáp án đúng: c
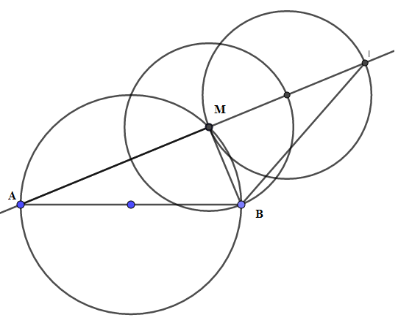
Tam giác $AMB$ vuông tại$M$ , ta có \(\widehat {AMB} = {90^0 }\). Mặt khác ta có: \(\widehat {AMB} + \widehat {IMB} = {180^0 },\) suy ra \(\widehat {IMB} = {90^0 }\)
hay tam giác $BMI$ vuông tại $M$ . Trong tam giác vuông $BMI$ ta có \(\tan\widehat {MIB} = \dfrac{{MB}}{{MI}} = \dfrac{1}{2}\)
Suy ra \(\widehat {MIB} = {a^0}\) không đổi hay \(\widehat {AIB} = {a^0}\) không đổi. Mà $A,B$ cố định
\( \Rightarrow \) Quỹ tích điểm $I$ là $2$ cung chứa góc \({a^0}\) dựng trên $AB$ với \(\tan a = \dfrac{1}{2}.\)
Hướng dẫn giải:
Sử dụng phương pháp cung chứa góc.
Hai điểm $B,C$ cố định. Quỹ tích các điểm $M$ thỏa mãn \(\widehat {BMC} = \alpha \) không đổi là $2$ cung chứa góc \(\alpha \) dựng trên$BC$ .
