Trả lời bởi giáo viên
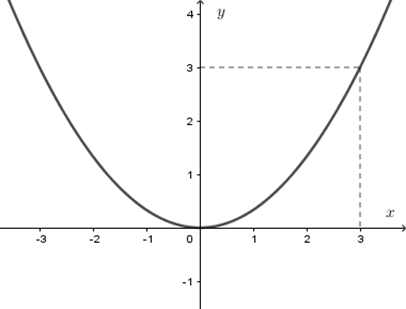
Từ hình vẽ ta thấy đồ thị đi qua điểm có tọa độ \(\left( {3;3} \right)\), ta thay \(x = 3;y = 3\) vào từng hàm số ở các đáp án ta được:
+ Đáp án A: \(y = {x^2} \Leftrightarrow 3 = {3^2} \Leftrightarrow 3 = 9\) (vô lý) nên loại A.
+ Đáp án B: \(y = \dfrac{1}{2}{x^2} \Leftrightarrow 3 = \dfrac{1}{2}{3^2} \Leftrightarrow 3 = \dfrac{9}{2}\) (vô lý) nên loại B.
+ Đáp án C: \(y = 3{x^2} \Leftrightarrow 3 = {3.3^2} \Leftrightarrow 3 = 27\) (vô lý) nên loại C.
+ Đáp án D: \(y = \dfrac{1}{3}{x^2} \Leftrightarrow 3 = \dfrac{1}{3}{.3^2} \Leftrightarrow 3 = 3\) (luôn đúng) nên chọn D.
Hướng dẫn giải:
Ta sử dụng các kiến thức sau:
* Đồ thị của hàm số \(y = a{x^2}\,\,\left( {a \ne 0} \right)\) là một đường cong (parabol) đi qua gốc tọa độ \(O\).
- Nếu \(a > 0\) thì đồ thị nằm phía trên trục hoành, O là điểm thấp nhất của đồ thị.
- Nếu \(a < 0\) thì đồ thị nằm phía dưới trục hoành, O là điểm cao nhất của đồ thị.
* Đồ thị hàm số \(y = a{x^2}\left( {a \ne 0} \right)\) đi qua điểm \(A\left( {{x_0};{y_0}} \right)\) khi \({y_0} = a{x_o}^2\)
Câu hỏi khác
- Bài tập hàm số bậc hai một ẩn và đồ thị hàm số y=ax^2 toán 9 có lời giải
- Bài tập hệ thức vi-ét và ứng dụng toán 9 có lời giải
- Bài tập phương trình bậc hai một ẩn và công thức nghiệm toán 9 có lời giải
- Bài tập công thức nghiệm thu gọn toán 9 có lời giải
- Bài tập phương trình quy về phương trình bậc hai toán 9 có lời giải
