Câu hỏi:
2 năm trước
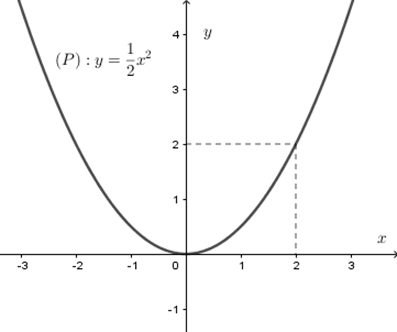
Cho đồ thị hàm số \(y = \dfrac{1}{2}{x^2}\) \(\left( P \right)\) như hình vẽ. Dựa vào đồ thị, tìm \(m\) để phương trình \({x^2} - 2m + 4 = 0\) có hai nghiệm phân biệt.
Trả lời bởi giáo viên
Đáp án đúng: a
Xét phương trình \({x^2} - 2m + 4 = 0\) (*) \( \Leftrightarrow {x^2} = 2m - 4 \Leftrightarrow \dfrac{1}{2}{x^2} = m - 2\)
Số nghiệm của phương trình (*) là số giao điểm của parabol \(\left( P \right):y = \dfrac{1}{2}{x^2}\) và đường thẳng \(d:y = m - 2\).
Để (*) có hai nghiệm phân biệt thì \(d\) cắt \(\left( P \right)\) tại hai điểm phân biệt.
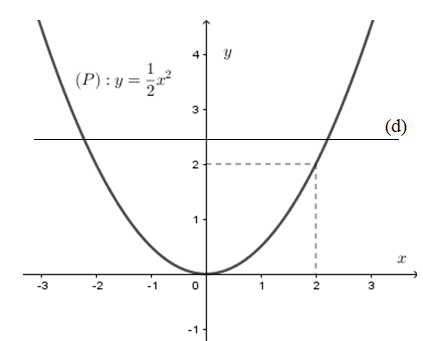
Từ đồ thị hàm số ta thấy:
Với \(m - 2 > 0 \Leftrightarrow m > 2\) thì \(d\) cắt \(\left( P \right)\) tại hai điểm phân biệt hay phương trình (*) có hai nghiệm phân biệt khi \(m > 2\).
Hướng dẫn giải:
Đưa phương trình về dạng \({\rm{a}}{{\rm{x}}^2} = mx + n\) (*)
Gọi parabol \(\left( P \right):y = a{x^2}\) và đường thẳng \(d:y = mx + n\)
Số nghiệm của (*) bằng đúng số giao điểm của d và (P).
- Nếu \((d)\) không cắt \((P)\) thì (*) vô nghiệm
- Nếu \((d)\) tiếp xúc với \((P)\) thì (*) có nghiệm kép
- Nếu \((d)\) cắt \((P)\) tại hai điểm phân biệt thì (*) có 2 nghiệm phân biệt .
Câu hỏi khác
- Bài tập hàm số bậc hai một ẩn và đồ thị hàm số y=ax^2 toán 9 có lời giải
- Bài tập hệ thức vi-ét và ứng dụng toán 9 có lời giải
- Bài tập phương trình bậc hai một ẩn và công thức nghiệm toán 9 có lời giải
- Bài tập công thức nghiệm thu gọn toán 9 có lời giải
- Bài tập phương trình quy về phương trình bậc hai toán 9 có lời giải
